Bagaimana cara mencari range dalam matematika

Matematika

Range dalam matematika adalah istilah yang digunakan untuk menggambarkan selisih antara nilai maksimum dan minimum dalam suatu himpunan data atau fungsi. Dalam konteks fungsi, range merujuk pada semua nilai output yang mungkin dihasilkan oleh fungsi tersebut. Memahami cara mencari range sangat penting dalam analisis data, statistik, dan kalkulus. Dalam artikel ini, kita akan membahas secara mendetail tentang cara mencari range, baik dalam konteks data numerik maupun fungsi matematis, disertai dengan penjelasan ilustratif untuk setiap konsep.

1. Pengertian Range

Range adalah ukuran yang menunjukkan seberapa jauh nilai-nilai dalam suatu himpunan data tersebar. Dalam istilah sederhana, range dapat didefinisikan sebagai selisih antara nilai tertinggi dan nilai terendah dalam suatu set data. Dalam konteks fungsi, range adalah himpunan semua nilai output (y) yang dihasilkan oleh fungsi tersebut untuk semua nilai input (x).

Ilustrasi Konsep

Bayangkan range sebagai jarak antara dua titik di sepanjang garis. Jika satu titik berada di 2 dan titik lainnya berada di 10, maka jarak (range) antara kedua titik tersebut adalah 8. Dalam konteks fungsi, bayangkan range sebagai semua titik yang dapat dicapai oleh sebuah bus yang bergerak di sepanjang jalan. Setiap pemberhentian bus mewakili nilai output yang dapat dicapai.

2. Mencari Range dari Himpunan Data

Untuk mencari range dari himpunan data, Anda dapat mengikuti langkah-langkah berikut:

a. Identifikasi Nilai Tertinggi dan Terendah

Langkah pertama adalah mengidentifikasi nilai maksimum (tertinggi) dan nilai minimum (terendah) dalam himpunan data.

Contoh: Misalkan kita memiliki himpunan data berikut: {3, 7, 2, 9, 5}. Dalam himpunan ini, nilai tertinggi adalah 9 dan nilai terendah adalah 2.

Ilustrasi Konsep

Bayangkan himpunan data sebagai sekumpulan bola berwarna yang diletakkan di atas meja. Bola dengan warna paling cerah mewakili nilai tertinggi, sementara bola dengan warna paling gelap mewakili nilai terendah. Dengan melihat semua bola, kita dapat dengan mudah mengidentifikasi mana yang paling tinggi dan paling rendah.

b. Hitung Range

Setelah menemukan nilai tertinggi dan terendah, Anda dapat menghitung range dengan menggunakan rumus berikut:

    \[ \text{Range} = \text{Nilai Tertinggi} - \text{Nilai Terendah} \]

Contoh: Menggunakan data di atas, kita dapat menghitung range sebagai berikut:

    \[ \text{Range} = 9 - 2 = 7 \]

Ilustrasi Konsep

Bayangkan Anda mengukur panjang sebuah papan kayu. Jika papan tersebut memiliki panjang 9 meter di satu ujung dan 2 meter di ujung lainnya, maka panjang papan kayu tersebut (range) adalah 7 meter. Ini menunjukkan seberapa jauh papan tersebut membentang.

3. Mencari Range dari Fungsi

Untuk mencari range dari fungsi matematis, langkah-langkahnya sedikit berbeda. Berikut adalah cara untuk melakukannya:

a. Tentukan Fungsi

Langkah pertama adalah menentukan fungsi yang ingin Anda analisis. Misalkan kita memiliki fungsi sederhana:

    \[ f(x) = x^2 \]

Ilustrasi Konsep

Bayangkan fungsi sebagai sebuah mesin. Ketika Anda memasukkan nilai (input) ke dalam mesin, mesin tersebut akan memproses nilai tersebut dan menghasilkan output. Dalam contoh ini, mesin mengubah nilai x menjadi x^2.

b. Temukan Nilai Minimum dan Maksimum

Untuk fungsi kuadrat seperti f(x) = x^2, kita perlu mencari nilai minimum dan maksimum. Dalam hal ini, fungsi kuadrat memiliki bentuk parabola yang terbuka ke atas, sehingga nilai minimum terjadi pada titik puncak.

  • Nilai Minimum: Untuk fungsi 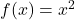f(x) = x^2, nilai minimum terjadi ketika 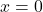x = 0, sehingga f(0) = 0^2 = 0.
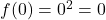  • Nilai Maksimum: Karena fungsi ini tidak memiliki batas atas (nilai x dapat terus bertambah), maka nilai maksimum tidak terdefinisi (infinity).

Ilustrasi Konsep

Bayangkan fungsi kuadrat sebagai sebuah lembah. Titik terendah di lembah adalah nilai minimum, sementara sisi-sisi lembah dapat terus menjulang tinggi tanpa batas. Ini menunjukkan bahwa meskipun ada titik terendah, tidak ada batasan untuk seberapa tinggi nilai output dapat mencapai.

c. Tentukan Range

Setelah menemukan nilai minimum dan maksimum, Anda dapat menentukan range. Dalam contoh ini, range dari fungsi f(x) = x^2 adalah:

    \[ \text{Range} = [0, \infty) \]

Ini berarti bahwa output dari fungsi ini dimulai dari 0 dan dapat terus meningkat tanpa batas.

Ilustrasi Konsep

Bayangkan range sebagai sebuah jalan yang dimulai dari titik nol dan terus membentang ke arah tak terhingga. Anda dapat berjalan di sepanjang jalan ini tanpa pernah menemukan akhir, yang mencerminkan bahwa nilai output dapat terus meningkat.

4. Kesimpulan

Mencari range dalam matematika adalah proses yang penting untuk memahami sebaran nilai dalam himpunan data atau fungsi. Dengan mengikuti langkah-langkah yang telah dijelaskan, Anda dapat dengan mudah menentukan range dari himpunan data maupun fungsi matematis. Range memberikan informasi yang berharga tentang seberapa jauh nilai-nilai dalam suatu set data tersebar dan membantu dalam analisis statistik dan matematis. Mari kita terus berlatih dan menerapkan konsep ini dalam berbagai konteks untuk meningkatkan pemahaman kita tentang matematika!