Volume adalah ukuran ruang tiga dimensi yang ditempati oleh suatu benda. Menghitung volume benda sangat penting dalam berbagai bidang, termasuk fisika, teknik, arsitektur, dan bahkan dalam kehidupan sehari-hari. Volume dapat dihitung untuk berbagai bentuk, baik itu bentuk geometris sederhana seperti kubus dan silinder, maupun bentuk yang lebih kompleks. Artikel ini akan membahas secara mendetail tentang bagaimana cara menghitung volume benda, rumus yang digunakan untuk berbagai bentuk, serta aplikasinya dalam kehidupan sehari-hari.
1. Definisi Volume
a. Pengertian Volume
Volume adalah ukuran kapasitas ruang yang ditempati oleh suatu benda. Dalam fisika, volume diukur dalam satuan kubik, seperti meter kubik (m³), liter (L), atau sentimeter kubik (cm³). Volume memberikan informasi tentang seberapa banyak zat atau material yang dapat dimuat dalam suatu wadah atau ruang.
b. Satuan Volume
Satuan volume dalam Sistem Internasional (SI) adalah meter kubik (m³). Namun, dalam praktik sehari-hari, kita sering menggunakan liter (1 liter = 1.000 cm³) atau sentimeter kubik (cm³) untuk mengukur volume cairan atau benda padat.
2. Menghitung Volume Benda Berdasarkan Bentuk Geometris
a. Volume Kubus
Kubus adalah bentuk tiga dimensi yang memiliki enam sisi yang sama. Rumus untuk menghitung volume kubus adalah:
![\[ V = s^3 \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc310fe95.png "Rendered by QuickLaTeX.com")
Di mana:
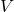= volume kubus (dalam m³ atau cm³)
= panjang sisi kubus (dalam m atau cm)
Contoh Perhitungan: Jika panjang sisi kubus adalah 3 cm, maka volume kubus dapat dihitung sebagai berikut:
![\[ V = 3^3 = 27 \, \text{cm}^3 \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc32077b2.png "Rendered by QuickLaTeX.com")
b. Volume Balok
Balok adalah bentuk tiga dimensi yang memiliki panjang, lebar, dan tinggi yang berbeda. Rumus untuk menghitung volume balok adalah:
![\[ V = p \times l \times t \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc3228752.png "Rendered by QuickLaTeX.com")
Di mana:
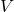- = volume balok (dalam m³ atau cm³)
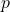= panjang balok (dalam m atau cm)
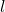= lebar balok (dalam m atau cm)
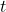= tinggi balok (dalam m atau cm)
Contoh Perhitungan: Jika panjang balok adalah 4 cm, lebar 3 cm, dan tinggi 2 cm, maka volume balok dapat dihitung sebagai berikut:
![\[ V = 4 \times 3 \times 2 = 24 \, \text{cm}^3 \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc3373f4a.png "Rendered by QuickLaTeX.com")
c. Volume Silinder
Silinder adalah bentuk tiga dimensi yang memiliki dua alas berbentuk lingkaran dan tinggi. Rumus untuk menghitung volume silinder adalah:
![\[ V = \pi r^2 t \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc3425215.png "Rendered by QuickLaTeX.com")
Di mana:
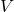- = volume silinder (dalam m³ atau cm³)
= jari-jari alas silinder (dalam m atau cm)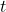- = tinggi silinder (dalam m atau cm)
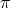= konstanta pi (sekitar 3,14)
Contoh Perhitungan: Jika jari-jari alas silinder adalah 2 cm dan tinggi silinder adalah 5 cm, maka volume silinder dapat dihitung sebagai berikut:
![\[ V = \pi \times 2^2 \times 5 \approx 3,14 \times 4 \times 5 \approx 62,8 \, \text{cm}^3 \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc34d6553.png "Rendered by QuickLaTeX.com")
d. Volume Kerucut
Kerucut adalah bentuk tiga dimensi yang memiliki alas berbentuk lingkaran dan satu titik puncak. Rumus untuk menghitung volume kerucut adalah:
![\[ V = \frac{1}{3} \pi r^2 t \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc3502f09.png "Rendered by QuickLaTeX.com")
Di mana:
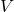- = volume kerucut (dalam m³ atau cm³)
- = jari-jari alas kerucut (dalam m atau cm)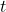
- = tinggi kerucut (dalam m atau cm)
Contoh Perhitungan: Jika jari-jari alas kerucut adalah 3 cm dan tinggi kerucut adalah 4 cm, maka volume kerucut dapat dihitung sebagai berikut:
![\[ V = \frac{1}{3} \pi \times 3^2 \times 4 \approx \frac{1}{3} \times 3,14 \times 9 \times 4 \approx 37,68 \, \text{cm}^3 \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc352b27b.png "Rendered by QuickLaTeX.com")
e. Volume Bola
Bola adalah bentuk tiga dimensi yang sempurna, di mana semua titik pada permukaan bola memiliki jarak yang sama dari pusat. Rumus untuk menghitung volume bola adalah:
![\[ V = \frac{4}{3} \pi r^3 \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc354a277.png "Rendered by QuickLaTeX.com")
Di mana:
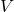- = volume bola (dalam m³ atau cm³)
- = jari-jari bola (dalam m atau cm)
Contoh Perhitungan: Jika jari-jari bola adalah 5 cm, maka volume bola dapat dihitung sebagai berikut:
![\[ V = \frac{4}{3} \pi \times 5^3 \approx \frac{4}{3} \times 3,14 \times 125 \approx 523,33 \, \text{cm}^3 \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc35648ae.png "Rendered by QuickLaTeX.com")
3. Menghitung Volume Benda dengan Bentuk Tidak Teratur
a. Metode Displacement
Untuk benda dengan bentuk tidak teratur, volume dapat dihitung menggunakan metode displacement. Metode ini melibatkan pengukuran perubahan volume cairan ketika benda dimasukkan ke dalam cairan. Langkah-langkahnya adalah sebagai berikut:
1. Isi wadah dengan cairan (misalnya air) hingga mencapai level tertentu dan catat volume awal.
2. Masukkan benda yang akan diukur ke dalam cairan.
3. Catat volume cairan setelah benda dimasukkan.
4. Hitung volume benda dengan mengurangkan volume awal dari volume akhir.
Contoh Perhitungan: Jika volume awal air dalam wadah adalah 200 mL dan setelah memasukkan benda, volume air menjadi 300 mL, maka volume benda tersebut adalah:
![\[ \text{Volume Benda} = \text{Volume Akhir} - \text{Volume Awal} = 300 \, \text{mL} - 200 \, \text{mL} = 100 \, \text{mL} \]](https://pengayaan.com/wp-content/uploads/2025/07/img_6871cc359d28c.png "Rendered by QuickLaTeX.com")
4. Aplikasi Menghitung Volume dalam Kehidupan Sehari-hari
a. Dalam Memasak
Menghitung volume sangat penting dalam memasak, terutama saat mengukur bahan cair atau padat. Misalnya, saat membuat adonan kue, kita perlu mengetahui volume bahan untuk mendapatkan proporsi yang tepat.
b. Dalam Konstruksi
Dalam konstruksi, menghitung volume material seperti beton, pasir, dan batu bata sangat penting untuk menentukan jumlah material yang diperlukan untuk proyek. Ini membantu dalam perencanaan dan penganggaran.
c. Dalam Ilmu Lingkungan
Menghitung volume juga penting dalam ilmu lingkungan, seperti dalam pengukuran volume air di danau atau sungai. Ini membantu dalam analisis kualitas air dan pengelolaan sumber daya air.
d. Dalam Pendidikan
Menghitung volume adalah bagian penting dari kurikulum pendidikan, terutama dalam pelajaran matematika dan fisika. Memahami konsep volume membantu siswa dalam mengembangkan keterampilan analitis dan pemecahan masalah.
5. Kesimpulan
Menghitung volume benda adalah proses penting yang melibatkan penggunaan rumus yang sesuai berdasarkan bentuk geometris benda. Dengan memahami cara menghitung volume untuk berbagai bentuk, kita dapat menerapkan pengetahuan ini dalam berbagai aspek kehidupan sehari-hari, mulai dari memasak hingga konstruksi dan ilmu lingkungan. Volume bukan hanya sekadar angka, tetapi juga merupakan bagian integral dari banyak fenomena yang mempengaruhi kehidupan kita. Dengan keterampilan menghitung volume, kita dapat lebih baik dalam merencanakan, menganalisis, dan memahami dunia di sekitar kita.