Acceleration is a fundamental concept in physics that describes the rate of change of velocity of an object with respect to time. It is a vector quantity, meaning it has both magnitude and direction. Understanding acceleration is crucial for analyzing motion, as it provides insights into how objects move and interact under the influence of various forces. This comprehensive overview will explore the definition of acceleration, its types, mathematical representation, factors affecting acceleration, applications, and its significance in various fields.
1. Definition of Acceleration
Acceleration is defined as the change in velocity per unit time. Mathematically, it can be expressed as:
![\[ a = \frac{\Delta v}{\Delta t} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-73c5bd4d18b59179d791f62231fe524f_l3.png "Rendered by QuickLaTeX.com")
Where:
= acceleration
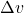= change in velocity (final velocity 
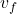minus initial velocity 
)
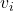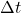= change in time
Acceleration can be positive, negative, or zero:
- Positive Acceleration: When an object speeds up, its acceleration is positive.
- Negative Acceleration (Deceleration): When an object slows down, its acceleration is negative.
- Zero Acceleration: When an object moves at a constant velocity, its acceleration is zero.
2. Types of Acceleration
Acceleration can be classified into several types based on the nature of the motion:
A. Uniform Acceleration:
Uniform acceleration occurs when an object experiences a constant acceleration over time. In this case, the velocity changes at a constant rate. An example of uniform acceleration is an object in free fall near the Earth’s surface, where it accelerates at approximately 
due to gravity.
B. Non-Uniform Acceleration:
Non-uniform acceleration occurs when the acceleration of an object changes over time. This can happen in various scenarios, such as a car accelerating while driving on a winding road or a roller coaster moving along a track.
C. Centripetal Acceleration:
Centripetal acceleration is the acceleration experienced by an object moving in a circular path. It is directed toward the center of the circular path and is given by the formula:
![\[ a_c = \frac{v^2}{r} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-5cbf0fb1c691874eec78bc487a2581f2_l3.png "Rendered by QuickLaTeX.com")
Where:
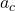= centripetal acceleration
= tangential velocity
= radius of the circular path
3. Mathematical Representation of Acceleration
Acceleration can be represented mathematically in various forms, depending on the context of the motion:
A. Average Acceleration:
The average acceleration over a time interval can be calculated using the formula:
![\[ a_{avg} = \frac{v_f - v_i}{t_f - t_i} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-71d56dc4784c0e1aa999547b5e8a5f88_l3.png "Rendered by QuickLaTeX.com")
B. Instantaneous Acceleration:
Instantaneous acceleration is the acceleration of an object at a specific moment in time. It can be determined by taking the derivative of the velocity function with respect to time:
![\[ a(t) = \frac{dv}{dt} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-6fee2585c92078e177555c52dca426d5_l3.png "Rendered by QuickLaTeX.com")
C. Kinematic Equations:
For uniformly accelerated motion, several kinematic equations relate acceleration to displacement, initial velocity, final velocity, and time. These equations are useful for solving problems involving linear motion:
1. 
2. 
3. 
Where:
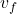= displacement- = final velocity
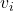- = initial velocity
- = acceleration
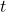= time
4. Factors Affecting Acceleration
Several factors influence the acceleration of an object:
A. Net Force:
According to Newton’s second law of motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This relationship can be expressed as:
![\[ F_{net} = m \cdot a \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-50687983cd2b0dec46446decfe33ac17_l3.png "Rendered by QuickLaTeX.com")
Where:
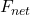= net force
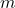= mass of the object- = acceleration
B. Mass of the Object:
The mass of an object affects its acceleration. A larger mass will experience less acceleration for the same amount of force applied, while a smaller mass will experience greater acceleration.
C. Friction and Resistance:
Frictional forces and air resistance can oppose the motion of an object, affecting its acceleration. The net force acting on the object must account for these opposing forces.
5. Applications of Acceleration
Acceleration has numerous applications across various fields:
A. Automotive Engineering:
In automotive engineering, understanding acceleration is crucial for designing vehicles that can accelerate quickly and safely. Engineers analyze acceleration to optimize performance, fuel efficiency, and safety features.
B. Sports Science:
In sports science, acceleration is a key factor in athletic performance. Coaches and trainers analyze the acceleration of athletes to improve their speed, agility, and overall performance in various sports.
C. Space Exploration:
In space exploration, acceleration plays a critical role in launching spacecraft and maneuvering them in space. Engineers must calculate the required acceleration to achieve desired trajectories and orbits.
D. Robotics:
In robotics, acceleration is essential for controlling the movement of robotic arms and vehicles. Understanding acceleration helps engineers design robots that can move efficiently and accurately.
6. Significance of Acceleration
Understanding acceleration is fundamental to the study of motion and dynamics. It provides insights into how objects respond to forces and how they move through space. Acceleration is a key concept in classical mechanics and serves as a foundation for more advanced topics in physics, such as kinematics, dynamics, and fluid mechanics. It is also essential for engineers, scientists, and anyone involved in fields that require the analysis of motion.
7. Conclusion
In conclusion, acceleration is a fundamental concept in physics that describes the rate of change of velocity of an object with respect to time. Its characteristics, mathematical representation, and factors affecting it provide a comprehensive understanding of how objects move and interact under the influence of forces. The applications of acceleration span various fields, from automotive engineering and sports science to space exploration and robotics. By studying acceleration, we gain valuable insights into the principles of motion and the forces that govern the behavior of objects in our world. Understanding these principles is essential for anyone involved in physics, engineering, and related disciplines, as they form the basis for analyzing and predicting the motion of objects in a wide range of scenarios.