Ampere’s Circuital Law is a fundamental principle in electromagnetism that relates the integrated magnetic field around a closed loop to the electric current passing through that loop. Named after the French physicist André-Marie Ampère, this law is a cornerstone of classical electromagnetism and plays a crucial role in understanding the behavior of magnetic fields generated by electric currents. This article delves into the formulation, implications, applications, and illustrative explanations of Ampere’s Circuital Law, providing a thorough understanding of this essential concept in physics.
The Mathematical Formulation of Ampere’s Circuital Law
Ampere’s Circuital Law can be mathematically expressed as:
![\[ \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-54b6ce56bebe60b31a8344998ebe7afd_l3.png "Rendered by QuickLaTeX.com")
Where:
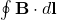represents the line integral of the magnetic field 
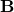around a closed loop.
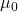is the permeability of free space, a constant that characterizes the ability of a vacuum to support magnetic fields, approximately equal to 
.
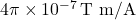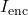is the total electric current enclosed by the loop.
Illustrative Explanation: Imagine a circular track (the closed loop) around which runners (the magnetic field lines) are moving. The total number of runners passing a specific point on the track (the line integral) is proportional to the number of spectators (the electric current) gathered inside the track. Just as the number of spectators influences the atmosphere of the event, the electric current influences the magnetic field around the loop.
Understanding the Components of Ampere’s Circuital Law
To fully grasp Ampere’s Circuital Law, it is essential to understand its key components: the magnetic field, the line integral, and the enclosed current.
1. Magnetic Field ()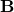
The magnetic field is a vector field that describes the magnetic influence of electric charges in relative motion and magnetized materials. It is represented by the symbol and is measured in teslas (T). The direction of the magnetic field is defined as the direction in which the north pole of a magnet would move.
Illustrative Explanation: Think of the magnetic field as the invisible lines of force surrounding a magnet. If you sprinkle iron filings around a magnet, they will align along these lines, visually demonstrating the magnetic field’s shape and direction. The strength of the magnetic field varies with distance from the magnet, just as the intensity of a light source diminishes with distance.
2. Line Integral ()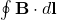
The line integral of the magnetic field around a closed loop quantifies the total magnetic field along that path. The integral sums the contributions of the magnetic field at each point along the loop, taking into account both the magnitude and direction of the field.
Illustrative Explanation: Imagine walking around a circular track while measuring the strength of the wind (the magnetic field) at various points. As you walk, you note how strong the wind feels at each location. The line integral is like adding up all those measurements to get a total wind effect around the track. If the wind blows consistently in one direction, the total effect will be significant; if it varies, the total may be less.
3. Enclosed Current ()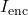
The enclosed current is the total electric current flowing through the area bounded by the closed loop. This current generates the magnetic field that is being measured. The relationship between the enclosed current and the magnetic field is what Ampere’s Circuital Law describes.
Illustrative Explanation: Picture a water pipe (the closed loop) with water flowing through it (the electric current). The amount of water flowing through the pipe affects the pressure and flow rate at various points along the pipe. Similarly, the amount of electric current flowing through the loop influences the strength of the magnetic field around it.
Implications of Ampere’s Circuital Law
Ampere’s Circuital Law has several important implications in the study of electromagnetism:
1. Magnetic Field Due to a Straight Conductor
One of the most common applications of Ampere’s Circuital Law is to determine the magnetic field generated by a long, straight current-carrying conductor. By applying the law to a circular loop centered around the wire, we can derive the expression for the magnetic field:
![\[ B = \frac{\mu_0 I}{2\pi r} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-d413d5e54370da8b67a7c4da4b696d3f_l3.png "Rendered by QuickLaTeX.com")
Where:
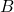is the magnetic field strength at a distance 
from the wire.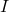
is the current flowing through the wire.
Illustrative Explanation: Imagine a straight wire carrying water (the current). As you move away from the wire, the flow of water (the magnetic field) becomes weaker. The farther you are from the wire, the less intense the water flow feels, similar to how the magnetic field strength decreases with distance from the current-carrying wire.
2. Magnetic Field in Solenoids
A solenoid is a coil of wire that generates a uniform magnetic field when an electric current passes through it. By applying Ampere’s Circuital Law to a solenoid, we can derive the expression for the magnetic field inside the solenoid:
![\[ B = \mu_0 n I \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-b031b35903cf8d1790baa7d2a9685a34_l3.png "Rendered by QuickLaTeX.com")
Where:
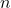is the number of turns per unit length of the solenoid.
Illustrative Explanation: Think of a solenoid as a tightly wound spring (the coil of wire) with water flowing through it (the current). The more tightly you wind the spring (more turns), the stronger the flow of water (magnetic field) becomes inside the spring. The uniformity of the magnetic field inside the solenoid is akin to the consistent flow of water throughout the length of the spring.
3. Ampere’s Law and Magnetic Materials
Ampere’s Circuital Law also applies to magnetic materials, where the magnetic field is influenced not only by the electric current but also by the magnetic properties of the material. In such cases, the law can be modified to include the magnetization of the material.
Illustrative Explanation: Imagine a sponge (the magnetic material) soaking up water (the magnetic field). The sponge’s ability to hold water (magnetization) affects how much water is present in the surrounding area (the magnetic field). The interaction between the current and the magnetic properties of the material leads to a more complex understanding of the magnetic field in such systems.
Applications of Ampere’s Circuital Law
Ampere’s Circuital Law has numerous practical applications across various fields, including:
1. Electrical Engineering
In electrical engineering, Ampere’s Circuital Law is used to design and analyze circuits, particularly in the context of inductors and transformers. Understanding how magnetic fields interact with electric currents is essential for developing efficient electrical devices.
Illustrative Explanation: Think of electrical engineers as architects designing buildings (circuits). Just as architects must consider how the structure will withstand forces (magnetic fields), engineers must understand how currents and magnetic fields interact to create efficient and reliable electrical systems.
2. Magnetic Field Mapping
Ampere’s Circuital Law is employed in magnetic field mapping, which is crucial for applications such as magnetic resonance imaging (MRI) and magnetic field sensors. By understanding the relationship between current and magnetic fields, scientists can create detailed maps of magnetic fields in various environments.
Illustrative Explanation: Imagine a treasure map (magnetic field map) that shows where the magnetic fields are strongest (treasures). By using Ampere’s Circuital Law, scientists can create accurate maps that help locate and understand the distribution of magnetic fields, much like following a treasure map to find hidden riches.
3. Electromagnetic Devices
Ampere’s Circuital Law is fundamental in the design of electromagnetic devices, such as electric motors, generators, and relays. These devices rely on the interaction between electric currents and magnetic fields to function effectively.
Illustrative Explanation: Think of an electric motor as a dance performance where dancers (electric currents) move in sync with the music (magnetic fields). The coordination between the dancers and the music creates a beautiful performance (the motor’s operation). Understanding Ampere’s Circuital Law allows engineers to design motors that operate smoothly and efficiently.
Conclusion
In conclusion, Ampere’s Circuital Law is a fundamental principle in electromagnetism that describes the relationship between the magnetic field around a closed loop and the electric current passing through that loop. By understanding the components of the law, including the magnetic field, line integral, and enclosed current, we can gain valuable insights into the behavior of magnetic fields generated by electric currents. The implications of Ampere’s Circuital Law extend to various applications in electrical engineering, magnetic field mapping, and the design of electromagnetic devices. As we continue to explore the intricate world of electromagnetism, Ampere’s Circuital Law remains a cornerstone of our understanding, illuminating the profound connections between electricity and magnetism that govern the behavior of the physical world. Through ongoing research and innovation, the principles of Ampere’s Circuital Law will undoubtedly continue to play a pivotal role in advancing our understanding of electromagnetism and its applications in modern technology.