Angular Velocity – Blog.Pengayaan.Com

Angular velocity is a fundamental concept in physics and engineering that describes the rate of rotation of an object around a specific axis. It is a vector quantity that provides information about how quickly an object is rotating and the direction of that rotation. Angular velocity is crucial in various fields, including mechanics, robotics, aerospace, and even in everyday applications such as the motion of wheels and gears. This article aims to provide an exhaustive overview of angular velocity, including its definition, significance, mathematical representation, measurement, applications, and illustrative explanations of each concept.

Definition of Angular Velocity

Angular velocity ( $\omega$ ) is defined as the rate of change of angular displacement with respect to time. It indicates how fast an object rotates around a specific axis and is typically measured in radians per second (rad/s). Mathematically, angular velocity can be expressed as:

$\omega = \frac{\Delta \theta}{\Delta t}$

Where:

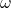$\omega$ is the angular velocity (in radians per second, rad/s),
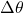$\Delta \theta$ is the change in angular position (in radians),
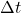$\Delta t$ is the change in time (in seconds).

Angular velocity can also be represented as a vector quantity, where the direction of the vector is along the axis of rotation, following the right-hand rule.

Significance of Angular Velocity

Angular velocity is significant for several reasons:

1. Understanding Rotational Motion: Angular velocity is essential for analyzing the motion of rotating objects. It helps describe how quickly an object is spinning and is a key parameter in the study of dynamics and kinematics.

2. Engineering Applications: In engineering, angular velocity is crucial for designing and analyzing systems involving rotational motion, such as gears, turbines, and motors. Understanding angular velocity allows engineers to optimize performance and efficiency.

3. Robotics and Control Systems: In robotics, angular velocity is vital for controlling the movement of robotic arms and joints. Accurate measurement and control of angular velocity enable precise positioning and manipulation of objects.

4. Aerospace and Mechanical Systems: In aerospace engineering, angular velocity is used to analyze the rotation of aircraft and spacecraft. It is also important in mechanical systems, such as flywheels and gyroscopes, where rotational stability is critical.

Mathematical Representation of Angular Velocity

Angular velocity can be represented in various forms, depending on the context:

1. In Terms of Linear Velocity: The relationship between angular velocity and linear velocity ( $v$ ) can be expressed as:

$v = r \cdot \omega$

Where:

$v$ is the linear velocity (in meters per second, m/s),
$r$ is the radius or distance from the axis of rotation (in meters, m),
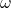$\omega$ is the angular velocity (in radians per second, rad/s).

Illustrative Example: Consider a point on the edge of a rotating disk with a radius of 0.5 meters. If the angular velocity of the disk is 4 rad/s, the linear velocity of the point can be calculated as:

$v = 0.5 \, \text{m} \cdot 4 \, \text{rad/s} = 2 \, \text{m/s}$

2. In Three-Dimensional Space: In three-dimensional space, angular velocity can be represented using a vector. The angular velocity vector ( $\vec{\omega}$ ) can be expressed in terms of its components along the x, y, and z axes:

$\vec{\omega} = \begin{pmatrix} \omega_x \\ \omega_y \\ \omega_z \end{pmatrix}$

Where $\omega_x$ , $\omega_y$ , and $\omega_z$ are the angular velocities about the respective axes.

3. In Terms of Frequency: Angular velocity can also be related to the frequency ( $f$ ) of rotation, which is the number of complete revolutions per unit time. The relationship is given by:

$\omega = 2\pi f$

Where:

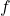$f$ is the frequency (in hertz, Hz).

Illustrative Example: If a wheel rotates at a frequency of 2 Hz, the angular velocity can be calculated as:

$\omega = 2\pi \cdot 2 \, \text{Hz} \approx 12.57 \, \text{rad/s}$

Measurement of Angular Velocity

Angular velocity can be measured using various methods and instruments, depending on the application:

1. Rotational Sensors: Devices such as rotary encoders and gyroscopes are commonly used to measure angular velocity. These sensors provide real-time data on the rotational speed and direction of an object.

Illustrative Example: A rotary encoder attached to a motor can measure the angular position of the motor shaft and calculate the angular velocity based on the change in position over time.

2. Video Analysis: In experimental settings, angular velocity can be measured by analyzing video footage of a rotating object. By tracking the angular displacement over time, the angular velocity can be calculated.

Illustrative Example: A researcher filming a spinning top can analyze the footage frame by frame to determine how many degrees the top rotates in a given time interval, allowing for the calculation of angular velocity.

3. Mathematical Calculations: In many engineering applications, angular velocity can be calculated using known parameters such as the radius of rotation and linear velocity, as previously discussed.

Applications of Angular Velocity

Angular velocity has numerous applications across various fields, including:

1. Mechanical Engineering: In mechanical systems, angular velocity is crucial for analyzing the performance of rotating machinery, such as turbines, engines, and gear systems. Engineers use angular velocity to optimize designs for efficiency and reliability.

Illustrative Example: In a wind turbine, the angular velocity of the blades is critical for maximizing energy capture from the wind. Engineers must design the turbine to operate at optimal angular velocities for different wind conditions.

2. Robotics: In robotics, angular velocity is essential for controlling the movement of robotic arms and joints. Accurate measurement of angular velocity allows for precise positioning and manipulation of objects.

Illustrative Example: A robotic arm used in manufacturing may have multiple joints that rotate. By controlling the angular velocity of each joint, the robot can perform complex tasks with high precision.

3. Aerospace Engineering: In aerospace applications, angular velocity is used to analyze the rotation of aircraft and spacecraft. It is critical for stability and control during flight.

Illustrative Example: In an aircraft, the angular velocity of the wings and tail surfaces affects the aircraft’s stability and maneuverability. Pilots and engineers must monitor and control these angular velocities during flight.

4. Sports Science: In sports, angular velocity is important for analyzing the performance of athletes. Understanding the angular velocity of limbs during activities such as throwing, swinging, or jumping can help improve techniques and performance.

Illustrative Example: A coach analyzing a baseball pitcher may measure the angular velocity of the pitcher’s arm during the throwing motion to identify areas for improvement in technique and power.

5. Entertainment and Animation: In the entertainment industry, angular velocity is used in animation and special effects to create realistic motion. Understanding how objects rotate and move is essential for creating believable animations.

Illustrative Example: In a computer-generated animation of a spinning planet, animators must calculate the angular velocity to ensure that the rotation appears natural and consistent with real-world physics.

Illustrative Explanations of Key Concepts

1. Right-Hand Rule: The right-hand rule is a convention used to determine the direction of the angular velocity vector. To apply the right-hand rule, point the thumb of your right hand in the direction of the axis of rotation, and curl your fingers in the direction of the rotation. The direction your thumb points indicates the direction of the angular velocity vector.

Illustrative Example: If you are looking down at a spinning top that rotates counterclockwise, you would point your right thumb upward (along the axis of rotation), indicating that the angular velocity vector points upward.

2. Centripetal Acceleration: When an object moves in a circular path, it experiences centripetal acceleration directed toward the center of the circle. The relationship between angular velocity and centripetal acceleration ( $a_c$ ) can be expressed as:

$a_c = r \cdot \omega^2$

Where:

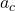$a_c$ is the centripetal acceleration (in meters per second squared, m/s²),
$r$ is the radius of the circular path (in meters, m),
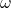$\omega$ is the angular velocity (in radians per second, rad/s).

Illustrative Example: A car traveling around a circular track experiences centripetal acceleration directed toward the center of the track. If the car has a radius of 50 meters and an angular velocity of 1 rad/s, the centripetal acceleration can be calculated as:

$a_c = 50 \, \text{m} \cdot (1 \, \text{rad/s})^2 = 50 \, \text{m/s}^2$

3. Angular Displacement: Angular displacement ( $\Delta \theta$ ) is the angle through which an object rotates about a specific axis. It is measured in radians and is a key component in calculating angular velocity.

Illustrative Example: If a Ferris wheel rotates from an initial angle of 0 radians to a final angle of $\pi$ radians (180 degrees), the angular displacement is:

$\Delta \theta = \pi - 0 = \pi \, \text{radians}$

4. Rotational Kinematics: Angular velocity is a key parameter in rotational kinematics, which describes the motion of rotating objects. The equations of motion for rotational systems are analogous to those for linear motion, allowing for the analysis of angular displacement, angular velocity, and angular acceleration.

Illustrative Example: If a spinning disk starts from rest and accelerates at a constant angular acceleration of 2 rad/s², the angular velocity after 5 seconds can be calculated using the equation:

$\omega = \omega_0 + \alpha t$

Where:

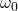$\omega_0$ is the initial angular velocity (0 rad/s),
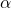$\alpha$ is the angular acceleration (2 rad/s²),
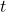$t$ is the time (5 s).

Thus,

$\omega = 0 + (2 \, \text{rad/s}^2)(5 \, \text{s}) = 10 \, \text{rad/s}$

Conclusion

Angular velocity is a fundamental concept that describes the rate of rotation of an object around a specific axis. Its definition, significance, mathematical representation, measurement, and applications provide valuable insights into the behavior of rotating systems. By examining key concepts such as the relationship between angular and linear velocity, the right-hand rule, centripetal acceleration, and rotational kinematics, we gain a deeper understanding of angular motion. The illustrative examples provided throughout the article highlight the practical implications of angular velocity in engineering, robotics, aerospace, sports science, and entertainment. As research continues to advance, the study of angular velocity will remain vital for developing new technologies, optimizing designs, and addressing challenges in rotational dynamics. Understanding angular velocity not only enriches our knowledge of motion but also contributes to innovations that enhance performance, safety, and efficiency across diverse applications.

Blog.Pengayaan.Com

Definition of Angular Velocity

Significance of Angular Velocity

Mathematical Representation of Angular Velocity

Measurement of Angular Velocity

Applications of Angular Velocity

Illustrative Explanations of Key Concepts

Conclusion

Leave a Reply Cancel reply