A rectangle is a fundamental geometric shape characterized by four sides, with opposite sides being equal in length and all interior angles measuring 
. Rectangles are ubiquitous in both nature and human-made structures, appearing in everything from buildings and furniture to art and design. Understanding the area of a rectangle is essential for various applications, including architecture, engineering, and everyday problem-solving. This article aims to provide an exhaustive overview of the area of a rectangle, detailing its definition, properties, formulas, applications, and illustrative explanations for each concept.
1. Definition of a Rectangle
A rectangle is defined as a quadrilateral (a four-sided polygon) with the following properties:
- Opposite Sides Equal: The lengths of opposite sides are equal. If we denote the length of the rectangle as
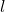and the width as 
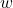, then:
![\[ \text{Length} = l \quad \text{and} \quad \text{Width} = w \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-78d4cc1955351a387bf13f1bce1d40ef_l3.png "Rendered by QuickLaTeX.com")
- Right Angles: Each of the four angles in a rectangle measures .
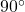1.1. Components of a Rectangle
- Length (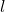): The longer side of the rectangle.
- Width (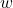): The shorter side of the rectangle.
- Diagonal: The diagonal of a rectangle can be calculated using the Pythagorean theorem, given by:
![\[ d = \sqrt{l^2 + w^2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-965d96e311a1d5b1da65f19dd5e4e122_l3.png "Rendered by QuickLaTeX.com")
2. Area of a Rectangle
The area of a rectangle is defined as the amount of space enclosed within its four sides. It can be calculated using the formula:
![\[ \text{Area} = l \times w \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e080425a1d3a43af326e5de4e6d4e9fa_l3.png "Rendered by QuickLaTeX.com")
where is the length and is the width.
2.1. Illustrative Explanation of Area Calculation
To visualize the area of a rectangle, consider a rectangle with a length of and a width of . The area can be thought of as the number of unit squares that can fit within the rectangle.
- Example: If we have a rectangle with a length of
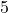units and a width of 
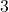units, we can visualize it as follows:
“` +——————-+ | | | | 3 units (width) | | +——————-+ 5 units (length) “`
To calculate the area, we multiply the length by the width:
![\[ \text{Area} = 5 \times 3 = 15 \, \text{square units} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-dbc550300eb3df7658d03f2b04778e30_l3.png "Rendered by QuickLaTeX.com")
This means that 
unit squares can fit within the rectangle.
2.2. Units of Area
The area of a rectangle is expressed in square units, which can vary depending on the measurement system used. Common units include:
- Square centimeters (
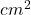) - Square meters (
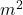) - Square inches (
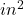) - Square feet (
)
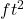When calculating the area, it is essential to ensure that the length and width are measured in the same unit to obtain a consistent area measurement.
3. Properties of Rectangles
Understanding the properties of rectangles is crucial for applying the area formula effectively. Here are some key properties:
3.1. Perimeter of a Rectangle
The perimeter of a rectangle is the total distance around the rectangle and can be calculated using the formula:
![\[ \text{Perimeter} = 2(l + w) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-799d5ca420e0cbf9ecbbd3c9dd1f52a3_l3.png "Rendered by QuickLaTeX.com")
- Illustrative Explanation: For a rectangle with a length of 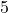units and a width of 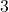units, the perimeter would be:
![\[ \text{Perimeter} = 2(5 + 3) = 2 \times 8 = 16 \, \text{units} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-74283dcfdc7f315372931429bdebb19d_l3.png "Rendered by QuickLaTeX.com")
3.2. Diagonal of a Rectangle
The diagonal of a rectangle can be calculated using the Pythagorean theorem, as mentioned earlier. The diagonal divides the rectangle into two right triangles.
- Illustrative Explanation: For a rectangle with a length of 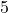units and a width of 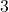units, the diagonal
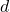can be calculated as follows:
![\[ d = \sqrt{l^2 + w^2} = \sqrt{5^2 + 3^2} = \sqrt{25 + 9} = \sqrt{34} \approx 5.83 \, \text{units} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-4f537e440c5ee1d998c53c0600844e83_l3.png "Rendered by QuickLaTeX.com")
3.3. Special Cases of Rectangles
- Square: A square is a special type of rectangle where all four sides are equal in length. In this case, the area can be calculated as:
![\[ \text{Area} = s^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ef2d94c3a6fb2e501b880922c8394214_l3.png "Rendered by QuickLaTeX.com")
where 
is the length of a side.
- Golden Rectangle: A golden rectangle has a length-to-width ratio of approximately
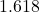, known as the golden ratio. This ratio is often found in nature and art.
4. Applications of the Area of a Rectangle
Understanding the area of a rectangle has numerous practical applications across various fields:
4.1. Architecture and Construction
In architecture and construction, calculating the area of rectangular spaces is essential for determining the amount of materials needed for flooring, walls, and roofing.
- Illustrative Explanation: If an architect is designing a room that is
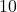meters long and 
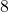meters wide, they can calculate the area to determine how much flooring material is required:
![\[ \text{Area} = 10 \times 8 = 80 \, m^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-cb629d588b3b5bcfe33f7b9d6d1b4ebf_l3.png "Rendered by QuickLaTeX.com")
4.2. Land Measurement
In land surveying, the area of rectangular plots is calculated to determine property sizes, land use, and agricultural planning.
- Illustrative Explanation: A farmer may have a rectangular field measuring
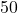meters by 
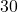meters. The area can be calculated to assess how much crop can be planted:
![\[ \text{Area} = 50 \times 30 = 1500 \, m^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e5bdb133db63d0a0a83fef41de21a5ba_l3.png "Rendered by QuickLaTeX.com")
4.3. Interior Design
Interior designers often use the area of rectangles to plan furniture arrangements, wall space, and room layouts.
- Illustrative Explanation: If a designer is planning to place a rug in a living room that is
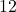feet long and 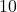feet wide, they can calculate the area to ensure the rug fits well:
![\[ \text{Area} = 12 \times 10 = 120 \, ft^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-944227549241340cf75157b39d93f639_l3.png "Rendered by QuickLaTeX.com")
4.4. Graphic Design
In graphic design, rectangles are commonly used in layouts, banners, and advertisements. Understanding the area helps designers create visually appealing compositions.
- Illustrative Explanation: A graphic designer may create a banner that is
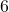feet wide and 
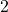feet tall. The area can be calculated to determine how much space the banner will occupy:
![\[ \text{Area} = 6 \times 2 = 12 \, ft^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d057e34cdda1baddcb61465f80a97acf_l3.png "Rendered by QuickLaTeX.com")
5. Example Problems
To further illustrate the concept of calculating the area of a rectangle, let’s consider a few example problems:
Example 1: Basic Area Calculation
Problem: Calculate the area of a rectangle with a length of 
cm and a width of 
cm.
Solution:
![\[ \text{Area} = l \times w = 7 \times 4 = 28 \, cm^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-565fbd9dfab1e1742f5a81ffa8514650_l3.png "Rendered by QuickLaTeX.com")
Example 2: Area of a Square
Problem: Find the area of a square with a side length of meters.
Solution:
![\[ \text{Area} = s^2 = 5^2 = 25 \, m^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-56fe58840396b5e7271de542a6acd353_l3.png "Rendered by QuickLaTeX.com")
Example 3: Real-World Application
Problem: A rectangular garden measures feet in length and feet in width. How much area is available for planting?
Solution:
![\[ \text{Area} = l \times w = 15 \times 10 = 150 \, ft^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-55eb95650cf4f22ea80243b4e7a3ca60_l3.png "Rendered by QuickLaTeX.com")
Conclusion
In conclusion, the area of a rectangle is a fundamental concept in geometry that is essential for various applications in architecture, construction, land measurement, interior design, and graphic design. By understanding the properties of rectangles and the formula for calculating area, one can effectively analyze and solve real-world problems involving rectangular shapes. The knowledge of rectangles and their areas is a key component of our mathematical toolkit, enabling us to make informed decisions in both professional and everyday contexts. As we continue to explore the vast landscape of geometry, the area of rectangles will remain a foundational concept that underpins many practical applications.