The trapezium, also known as a trapezoid in some regions, is a four-sided polygon (quadrilateral) characterized by at least one pair of parallel sides. The area of a trapezium is an important concept in geometry, with applications in various fields such as architecture, engineering, and design. This article aims to provide a detailed exploration of the area of a trapezium, including its definition, properties, formula for calculating the area, and illustrative explanations to enhance understanding.
1. Definition of a Trapezium
A trapezium is defined as a quadrilateral with at least one pair of parallel sides. The parallel sides are referred to as the “bases” of the trapezium, while the non-parallel sides are called the “legs.” Trapeziums can be classified into two main types:
- Isosceles Trapezium: A trapezium where the non-parallel sides (legs) are equal in length, and the angles adjacent to each base are equal.
- Scalene Trapezium: A trapezium where the non-parallel sides are of different lengths, and the angles are not necessarily equal.
Illustrative Explanation
To visualize a trapezium, imagine a shape like a table with a flat top and bottom. The top and bottom edges represent the parallel sides (bases), while the sides of the table represent the non-parallel sides (legs). For example, if you have a trapezium with a top base of 
and a bottom base of 
, the legs can be of different lengths, making it a scalene trapezium.
2. Properties of a Trapezium
Understanding the properties of a trapezium is essential for calculating its area. Here are some key properties:
- Parallel Sides: The two bases are parallel, which means they will never meet, regardless of how far they are extended.
- Height: The height (or altitude) of a trapezium is the perpendicular distance between the two bases. It is crucial for calculating the area.
- Angles: The angles adjacent to each base can vary, and in an isosceles trapezium, the angles at each base are equal.
Illustrative Explanation
Consider a trapezium with a top base of , a bottom base of , and a height of 
. The height can be visualized as a vertical line drawn from the top base to the bottom base, forming right angles with both bases. This height is essential for calculating the area.
3. Area Formula for a Trapezium
The area 
of a trapezium can be calculated using the following formula:
![\[ A = \frac{1}{2} \times (b_1 + b_2) \times h \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-127252d241cc8b68d147d6d2465c577a_l3.png "Rendered by QuickLaTeX.com")
Where:
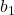= length of the first base (top base)
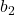= length of the second base (bottom base)
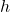= height of the trapezium
Example Calculation
Let’s say we have a trapezium with the following dimensions:
- Top base () =
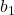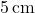
- Bottom base () =
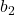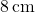
- Height () =
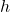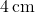
We can calculate the area as follows:
![\[ A = \frac{1}{2} \times (5 \, \text{cm} + 8 \, \text{cm}) \times 4 \, \text{cm}\ \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a3afbcafb140e3ad2305cba55c05bca3_l3.png "Rendered by QuickLaTeX.com")
Calculating the sum of the bases:
![\[ A = \frac{1}{2} \times 13 \, \text{cm} \times 4 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d474956a48b2370301a0fe954c2ca9c9_l3.png "Rendered by QuickLaTeX.com")
Now, multiplying:
![\[ A = \frac{1}{2} \times 52 \, \text{cm}^2 = 26 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-99a044142de66b64f986806bd7828313_l3.png "Rendered by QuickLaTeX.com")
Thus, the area of the trapezium is 
.
4. Visualizing the Area of a Trapezium
To further understand the area of a trapezium, it can be helpful to visualize it. Imagine cutting the trapezium into two triangles and a rectangle. By drawing a line from the top base to the bottom base, you can create two right triangles on either side of the rectangle formed by the height and the bases.
Illustrative Explanation
1. Draw the Trapezium: Start with a trapezium with a top base of and a bottom base of .
2. Identify the Height: Draw a vertical line from the top base to the bottom base, marking the height as .
3. Visualize the Components: The trapezium can be seen as a rectangle in the middle with a height of and a width equal to the difference in the lengths of the bases, plus two triangles on either side.
This visualization helps reinforce the idea that the area of the trapezium can be thought of as the sum of the areas of the rectangle and the two triangles.
5. Applications of the Area of a Trapezium
Understanding the area of a trapezium has practical applications in various fields:
5.1. Architecture and Construction
In architecture, trapeziums are often used in the design of roofs, bridges, and other structures. Calculating the area is essential for determining materials needed and ensuring structural integrity.
5.2. Land Measurement
In land surveying, plots of land can often take the shape of trapeziums. Knowing the area helps in assessing property values and planning land use.
5.3. Graphic Design
In graphic design, trapeziums can be used in layouts and designs. Understanding their area can help designers create balanced and aesthetically pleasing compositions.
6. Conclusion
The area of a trapezium is a fundamental concept in geometry that is essential for various applications in real life. By understanding the properties of trapeziums, the formula for calculating their area, and visualizing the components involved, one can confidently tackle problems related to trapeziums in mathematics and practical scenarios.
In summary, the area of a trapezium can be easily calculated using the formula 
. This knowledge not only enhances mathematical skills but also provides valuable insights into the design and measurement of various structures and spaces in the world around us. By mastering the area of trapeziums, one can appreciate the beauty and utility of geometry in everyday life.