Bernoulli’s Equation – Blog.Pengayaan.Com

Bernoulli’s Equation is a fundamental principle in fluid dynamics that describes the behavior of fluid flow and the relationship between pressure, velocity, and elevation in a moving fluid. Named after the Swiss mathematician Daniel Bernoulli, this equation is essential for understanding various phenomena in engineering, physics, and natural sciences. It provides insights into how fluids behave under different conditions and is widely applied in fields such as aerodynamics, hydrodynamics, and engineering design. This article aims to provide an exhaustive overview of Bernoulli’s Equation, including its derivation, significance, applications, and illustrative explanations of each concept.

Definition of Bernoulli’s Equation

Bernoulli’s Equation states that in a steady, incompressible flow of an ideal fluid with no friction, the total mechanical energy along a streamline is constant. The equation can be expressed mathematically as:

$P + \frac{1}{2} \rho v^2 + \rho gh = \text{constant}$

Where:

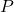$P$ is the static pressure of the fluid (in pascals, Pa),
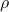$\rho$ is the fluid density (in kilograms per cubic meter, kg/m³),
$v$ is the flow velocity of the fluid (in meters per second, m/s),
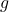$g$ is the acceleration due to gravity (approximately $9.81 \, \text{m/s}^2$ ),
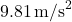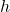$h$ is the height above a reference level (in meters, m).

The three terms in the equation represent different forms of energy per unit volume of the fluid:
1. Static Pressure Energy ( $P$ ): The energy associated with the pressure exerted by the fluid.
2. Dynamic Pressure Energy ( $\frac{1}{2} \rho v^2$ ): The kinetic energy per unit volume of the fluid due to its motion.
3. Gravitational Potential Energy ( $\rho gh$ ): The potential energy per unit volume of the fluid due to its elevation in a gravitational field.

Derivation of Bernoulli’s Equation

The derivation of Bernoulli’s Equation is based on the principle of conservation of energy. To derive the equation, consider a fluid flowing through a horizontal pipe with varying diameters. The following steps outline the derivation:

1. Consider a Fluid Element: Imagine a small fluid element of length $L$ and cross-sectional area $A$ moving through a pipe. The fluid element has a mass $m = \rho AL$ .

2. Apply the Work-Energy Principle: The work done on the fluid element by pressure forces can be expressed as the difference in pressure between the two ends of the element:

$W = (P_1 - P_2) A L$

Where $P_1$ and $P_2$ are the pressures at the two ends of the fluid element.

3. Relate Work to Energy: The work done on the fluid element results in a change in kinetic energy and potential energy. The change in kinetic energy ( $\Delta KE$ ) can be expressed as:

$\Delta KE = \frac{1}{2} m v_2^2 - \frac{1}{2} m v_1^2 = \frac{1}{2} \rho AL \left( v_2^2 - v_1^2 \right)$

The change in potential energy ( $\Delta PE$ ) can be expressed as:

$\Delta PE = mgh_2 - mgh_1 = \rho AL \left( gh_2 - gh_1 \right)$

4. Set Up the Energy Balance: According to the work-energy principle, the work done on the fluid element is equal to the change in kinetic energy plus the change in potential energy:

$(P_1 - P_2) A L = \frac{1}{2} \rho AL \left( v_2^2 - v_1^2 \right) + \rho AL \left( gh_2 - gh_1 \right)$

5. Simplify the Equation: Dividing through by $AL$ and rearranging gives:

$P_1 + \frac{1}{2} \rho v_1^2 + \rho gh_1 = P_2 + \frac{1}{2} \rho v_2^2 + \rho gh_2$

This is the general form of Bernoulli’s Equation, which states that the total mechanical energy along a streamline remains constant.

Significance of Bernoulli’s Equation

Bernoulli’s Equation is significant for several reasons:

1. Understanding Fluid Behavior: The equation provides a framework for understanding how fluids behave under varying conditions of pressure, velocity, and elevation. It helps explain phenomena such as lift generation in aircraft wings and the behavior of fluids in pipes.

2. Engineering Applications: Engineers use Bernoulli’s Equation to design systems involving fluid flow, such as water supply systems, HVAC systems, and aerodynamic structures. It aids in predicting how fluids will behave in different scenarios.

3. Predicting Flow Patterns: Bernoulli’s Equation allows for the prediction of flow patterns in various applications, including the design of nozzles, diffusers, and pumps. It helps engineers optimize designs for efficiency and performance.

4. Safety and Efficiency: Understanding the principles behind Bernoulli’s Equation can lead to safer and more efficient designs in various industries, including aerospace, automotive, and civil engineering.

Applications of Bernoulli’s Equation

Bernoulli’s Equation has numerous applications across various fields, including:

1. Aerospace Engineering: In aerodynamics, Bernoulli’s Equation is used to explain how lift is generated on an aircraft wing. The shape of the wing causes air to flow faster over the top surface than the bottom surface, resulting in lower pressure above the wing and higher pressure below, creating lift.

Illustrative Example: When an airplane takes off, the wings are designed to create a difference in airspeed above and below the wing. According to Bernoulli’s principle, the faster airflow over the top of the wing results in lower pressure, allowing the aircraft to rise.

2. Hydraulics: In hydraulic systems, Bernoulli’s Equation is used to analyze fluid flow in pipes and channels. It helps engineers design efficient systems for transporting water, oil, and other fluids.

Illustrative Example: In a water supply system, Bernoulli’s Equation can be used to determine the pressure drop along a pipe due to friction and changes in elevation, allowing engineers to size pumps and pipes appropriately.

3. Venturi Effect: The Venturi effect, which is a direct application of Bernoulli’s Equation, describes how fluid velocity increases as it passes through a constricted section of a pipe, resulting in a decrease in pressure. This principle is used in various applications, including carburetors and atomizers.

Illustrative Example: In a carburetor, air is drawn through a narrow passage, increasing its velocity and decreasing its pressure. This low pressure draws fuel into the airflow, mixing it with air to create a combustible mixture for an engine.

4. Flow Measurement: Bernoulli’s Equation is used in devices such as pitot tubes and orifice plates to measure fluid flow rates. These devices exploit the relationship between pressure and velocity to determine the flow rate of fluids in pipes and ducts.

Illustrative Example: A pitot tube is used in aviation to measure the airspeed of an aircraft. It measures the difference between static pressure and dynamic pressure, allowing pilots to determine their speed relative to the surrounding air.

5. Sports Science: In sports, Bernoulli’s Equation helps analyze the behavior of balls and other objects in motion. Understanding how air pressure affects the trajectory of a ball can improve performance in sports such as soccer, golf, and baseball.

Illustrative Example: When a soccer player kicks a ball with spin, the difference in air pressure on opposite sides of the ball causes it to curve in the air. This phenomenon can be explained using Bernoulli’s Equation and the principles of fluid dynamics.

Illustrative Explanations of Key Concepts

1. Static Pressure: Static pressure is the pressure exerted by a fluid at rest. It is the force per unit area exerted by the fluid on the walls of its container or on any surface in contact with it.

Illustrative Example: When you fill a balloon with air, the air inside exerts static pressure on the inner walls of the balloon. If you squeeze the balloon, you increase the static pressure inside, causing the balloon to expand.

2. Dynamic Pressure: Dynamic pressure is the pressure associated with the motion of a fluid. It is calculated using the formula $\frac{1}{2} \rho v^2$ and represents the kinetic energy per unit volume of the fluid.

Illustrative Example: When water flows through a garden hose, the faster the water moves, the higher the dynamic pressure. If you place your thumb over the end of the hose, the water speeds up, increasing the dynamic pressure and causing the water to shoot out farther when you remove your thumb.

3. Gravitational Potential Energy: Gravitational potential energy is the energy stored in an object due to its height above a reference level. In the context of Bernoulli’s Equation, it is represented by the term $\rho gh$ .

Illustrative Example: A water tank elevated above the ground has gravitational potential energy due to its height. When the water is released, it flows down due to gravity, converting potential energy into kinetic energy as it gains speed.

4. Conservation of Energy: Bernoulli’s Equation is based on the principle of conservation of energy, which states that energy cannot be created or destroyed, only transformed from one form to another. In fluid dynamics, the total mechanical energy of a fluid remains constant along a streamline.

Illustrative Example: Consider a roller coaster. As the coaster climbs to the top of a hill, it gains potential energy. As it descends, that potential energy is converted into kinetic energy, allowing the coaster to speed up. Similarly, in fluid flow, energy is transformed between pressure, kinetic, and potential forms.

Conclusion

Bernoulli’s Equation is a fundamental principle in fluid dynamics that describes the relationship between pressure, velocity, and elevation in a moving fluid. Its derivation, significance, applications, and illustrative explanations provide valuable insights into the behavior of fluids under various conditions. By understanding key concepts such as static pressure, dynamic pressure, gravitational potential energy, and the conservation of energy, we can appreciate the practical implications of Bernoulli’s Equation in engineering, aerodynamics, hydraulics, and everyday life. As research continues to advance, the study of fluid dynamics and Bernoulli’s Equation will remain vital for developing new technologies, optimizing designs, and addressing challenges in fluid flow and energy management. Understanding Bernoulli’s Equation not only enriches our knowledge of fluid behavior but also contributes to innovations that enhance efficiency, safety, and performance across diverse applications.

Blog.Pengayaan.Com