Branches of Mathematics: A Comprehensive Exploration

Mathematics is a vast and intricate field of study that encompasses a wide range of concepts, theories, and applications. It serves as the foundation for various disciplines, including science, engineering, economics, and social sciences. The beauty of mathematics lies in its ability to describe patterns, solve problems, and provide insights into the world around us. This article aims to provide an exhaustive overview of the major branches of mathematics, detailing their definitions, key concepts, properties, and illustrative explanations for each.

1. Arithmetic

1.1. Definition of Arithmetic

Arithmetic is the branch of mathematics that deals with the basic operations of numbers. It involves the study of addition, subtraction, multiplication, and division, as well as the properties and relationships of numbers.

1.2. Key Concepts in Arithmetic

Natural Numbers: The set of positive integers starting from 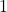$1$ (i.e., $1, 2, 3, \ldots$ ).
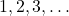Whole Numbers: The set of natural numbers including zero (i.e., $0, 1, 2, 3, \ldots$ ).
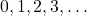Integers: The set of whole numbers and their negative counterparts (i.e., $\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots$ ).
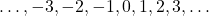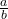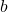Rational Numbers: Numbers that can be expressed as the quotient of two integers (i.e., $\frac{a}{b}$ , where $a$ and $b$ are integers and $b \neq 0$ ).
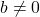Real Numbers: The set of all rational and irrational numbers, encompassing all points on the number line.

1.3. Illustrative Explanation

Consider the operation of addition:

$3 + 5 = 8$

In this example, $3$ and $5$ are added together to yield $8$ . This simple operation forms the basis of arithmetic and is foundational for more complex mathematical concepts.

2. Algebra

2.1. Definition of Algebra

Algebra is the branch of mathematics that deals with symbols and the rules for manipulating those symbols. It involves the study of mathematical expressions, equations, and functions, allowing for the representation of relationships between quantities.

2.2. Key Concepts in Algebra

Variables: Symbols (often letters) that represent unknown values (e.g., $x$ , $y$ ).
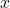Expressions: Combinations of numbers, variables, and operations (e.g., $2x + 3$ ).
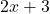Equations: Mathematical statements that assert the equality of two expressions (e.g., $2x + 3 = 7$ ).
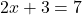Functions: Relationships between sets of inputs and outputs, often expressed as $f(x)$ .

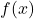2.3. Illustrative Explanation

Consider the equation:

$2x + 3 = 7$

To solve for $x$ , we can isolate the variable:

1. Subtract $3$ from both sides:

$2x = 4$

2. Divide by $2$ :

$x = 2$

This process illustrates how algebra allows us to manipulate symbols to find unknown values.

3. Geometry

3.1. Definition of Geometry

Geometry is the branch of mathematics that studies the properties and relationships of shapes, sizes, and figures in space. It encompasses both two-dimensional and three-dimensional objects.

3.2. Key Concepts in Geometry

Points: The most basic unit in geometry, representing a location in space with no dimensions.
Lines: Straight paths that extend infinitely in both directions, defined by two points.
Angles: The measure of rotation between two intersecting lines.
Shapes: Two-dimensional figures such as triangles, rectangles, and circles, as well as three-dimensional objects like cubes, spheres, and cylinders.

3.3. Illustrative Explanation

Consider a triangle with sides of lengths $3$ , $4$ , and $5$ . The area can be calculated using Heron’s formula:

1. Calculate the semi-perimeter $s$ :

$s = \frac{3 + 4 + 5}{2} = 6$

2. Use Heron’s formula:

$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{6(6-3)(6-4)(6-5)} = \sqrt{6 \cdot 3 \cdot 2 \cdot 1} = \sqrt{6 \cdot 6} = 6$

This example illustrates how geometry provides tools for calculating properties of shapes.

4. Trigonometry

4.1. Definition of Trigonometry

Trigonometry is the branch of mathematics that studies the relationships between the angles and sides of triangles, particularly right triangles. It is essential for understanding periodic phenomena and has applications in various fields, including physics and engineering.

4.2. Key Concepts in Trigonometry

Sine ( 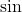$\sin$ ): The ratio of the length of the opposite side to the hypotenuse in a right triangle.
Cosine ( 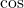$\cos$ ): The ratio of the length of the adjacent side to the hypotenuse.
Tangent ( 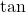$\tan$ ): The ratio of the length of the opposite side to the adjacent side.
Pythagorean Theorem: A fundamental relation in Euclidean geometry among the three sides of a right triangle, expressed as:

$a^2 + b^2 = c^2$

where $c$ is the hypotenuse.

4.3. Illustrative Explanation

Consider a right triangle with an angle $\theta$ :

If the length of the opposite side is 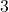$3$ and the hypotenuse is 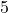$5$ , then:

$\sin(\theta) = \frac{3}{5}$

This relationship allows us to find unknown angles or side lengths in right triangles.

5. Calculus

5.1. Definition of Calculus

Calculus is the branch of mathematics that studies continuous change. It is divided into two main areas: differential calculus, which focuses on rates of change and slopes of curves, and integral calculus, which deals with the accumulation of quantities and areas under curves.

5.2. Key Concepts in Calculus

Limits: The value that a function approaches as the input approaches a certain point.
Derivatives: The measure of how a function changes as its input changes, representing the slope of the tangent line to a curve.
Integrals: The accumulation of quantities, representing the area under a curve.

5.3. Illustrative Explanation

Consider the function $f(x) = x^2$ . To find the derivative, we can use the limit definition:

$f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = \lim_{h \to 0} (2x + h) = 2x$

This shows how calculus allows us to analyze the behavior of functions.

6. Statistics and Probability

6.1. Definition of Statistics and Probability

Statistics is the branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. Probability, on the other hand, is the study of uncertainty and the likelihood of events occurring.

6.2. Key Concepts in Statistics and Probability

Mean: The average of a set of numbers, calculated by summing the values and dividing by the count.
Median: The middle value in a sorted list of numbers.
Mode: The value that appears most frequently in a data set.
Probability: A measure of the likelihood of an event occurring, expressed as a number between 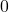$0$ and $1$ .

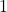6.3. Illustrative Explanation

Consider a data set: $2, 3, 5, 7, 7, 8$ .

Mean:

$\text{Mean} = \frac{2 + 3 + 5 + 7 + 7 + 8}{6} = \frac{32}{6} \approx 5.33$

Median: The middle value is 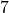$7$ (the average of the two middle numbers).
Mode: The most frequent value is $7$ .

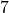In probability, if we flip a fair coin, the probability of getting heads is:

$P(\text{Heads}) = \frac{1}{2}$

This illustrates how statistics and probability help us analyze data and make informed decisions.

7. Discrete Mathematics

7.1. Definition of Discrete Mathematics

Discrete mathematics is the branch of mathematics that deals with countable, distinct, and separate objects. It includes topics such as graph theory, combinatorics, and number theory.

7.2. Key Concepts in Discrete Mathematics

Graphs: Structures consisting of vertices (nodes) connected by edges (lines).
Combinatorics: The study of counting, arrangement, and combination of objects.
Set Theory: The study of sets, which are collections of distinct objects.

7.3. Illustrative Explanation

Consider a simple graph with vertices $A$ , $B$ , and $C$ :

“`
 A
/ \
B—C
“`

In this graph, $A$ is connected to both $B$ and $C$ , while $B$ and $C$ are also connected. This structure allows us to analyze relationships and pathways within networks.

Conclusion

In conclusion, mathematics is a rich and diverse field that encompasses various branches, each with its own unique concepts, properties, and applications. From the foundational operations of arithmetic to the complexities of calculus and the intricacies of discrete mathematics, each branch plays a vital role in understanding and solving real-world problems. By exploring these branches, we gain valuable insights into the patterns and structures that govern our world, enabling us to make informed decisions and advance our knowledge across multiple disciplines. As we continue to delve into the vast landscape of mathematics, the understanding of its branches will remain a key component of our intellectual toolkit, empowering us to tackle challenges and explore new frontiers.

Blog.Pengayaan.Com