The bulk modulus of elasticity is a fundamental property of materials that quantifies their response to uniform pressure applied in all directions. It is a critical parameter in fields such as materials science, engineering, and geophysics, as it helps predict how materials will behave under various loading conditions. This article provides an in-depth examination of the bulk modulus of elasticity, including its definition, mathematical formulation, significance, applications, and illustrative explanations of each concept.
—
1. Definition of Bulk Modulus of Elasticity
The bulk modulus of elasticity (K) is defined as the measure of a material’s resistance to uniform compression. It quantifies how much a material will deform (change in volume) when subjected to an applied pressure. Mathematically, the bulk modulus is expressed as:
![]()
Where:
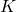 is the bulk modulus (in pascals, Pa),
is the bulk modulus (in pascals, Pa),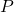 is the applied pressure (in pascals, Pa),
is the applied pressure (in pascals, Pa),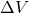 is the change in volume (in cubic meters, m³),
is the change in volume (in cubic meters, m³),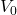 is the original volume (in cubic meters, m³).
is the original volume (in cubic meters, m³).
The negative sign indicates that an increase in pressure results in a decrease in volume, reflecting the inverse relationship between pressure and volume.
Illustrative Explanation:
Imagine a balloon filled with air. When you squeeze the balloon, you apply pressure to it. As a result, the volume of the balloon decreases. The bulk modulus of elasticity quantifies how much the volume decreases in response to the pressure you apply. A material with a high bulk modulus will compress less than a material with a low bulk modulus when subjected to the same pressure.
—
2. Mathematical Formulation of Bulk Modulus
The bulk modulus can also be expressed in terms of the change in pressure and the resulting change in volume:
![]()
Where:
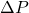 is the change in pressure,
is the change in pressure,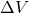 is the change in volume.
is the change in volume.
This formulation emphasizes that the bulk modulus is a measure of how much pressure is required to achieve a certain change in volume.
Illustrative Explanation:
Consider a metal cube submerged in water. If you apply pressure to the cube by increasing the water depth, the cube will experience a change in volume. The bulk modulus helps determine how much pressure is needed to achieve a specific volume change. For example, if the cube has a bulk modulus of 100 GPa, it will require a significant increase in pressure to produce a small change in volume.
—
3. Significance of Bulk Modulus of Elasticity
The bulk modulus of elasticity is significant for several reasons:
3.1 Material Selection
In engineering and construction, understanding the bulk modulus helps engineers select appropriate materials for specific applications. Materials with high bulk moduli are preferred in applications where resistance to compression is critical, such as in structural components, pressure vessels, and underwater structures.
Illustrative Explanation:
When designing a submarine, engineers must choose materials that can withstand the immense pressure of deep water. Materials with high bulk moduli, such as titanium or certain alloys, are selected to ensure the submarine maintains its structural integrity under high pressure.
3.2 Predicting Material Behavior
The bulk modulus allows engineers and scientists to predict how materials will behave under different loading conditions. This is essential for ensuring safety and performance in various applications, from aerospace to civil engineering.
Illustrative Explanation:
In the design of a bridge, engineers must consider how the materials will respond to the weight of vehicles and environmental factors. By knowing the bulk modulus of the materials used, they can predict how much the bridge will compress under load and ensure it remains safe for use.
3.3 Understanding Geological Processes
In geophysics, the bulk modulus is used to study the behavior of rocks and soils under pressure. It helps geologists understand how seismic waves propagate through the Earth and how geological formations respond to tectonic forces.
Illustrative Explanation:
When an earthquake occurs, seismic waves travel through the Earth’s crust. The bulk modulus of the rocks determines how these waves propagate. By studying the bulk modulus of different geological materials, scientists can better understand earthquake dynamics and assess potential hazards.
—
4. Applications of Bulk Modulus of Elasticity
The bulk modulus of elasticity has a wide range of applications across various fields:
4.1 Engineering and Construction
In civil engineering, the bulk modulus is crucial for designing structures that can withstand external pressures, such as buildings, bridges, and dams. Engineers use the bulk modulus to ensure that materials can handle the forces they will encounter during their lifespan.
Illustrative Explanation:
When constructing a dam, engineers must consider the pressure exerted by the water on the dam’s walls. By knowing the bulk modulus of the materials used in the dam, they can calculate how much the dam will compress under the weight of the water and design it to ensure stability.
4.2 Material Science
In materials science, the bulk modulus is used to characterize the mechanical properties of materials. Researchers study the bulk modulus to develop new materials with specific properties, such as lightweight composites or high-strength alloys.
Illustrative Explanation:
A materials scientist may experiment with different combinations of polymers and fibers to create a composite material with a high bulk modulus. This material could be used in aerospace applications where lightweight and strong materials are essential.
4.3 Acoustics
In acoustics, the bulk modulus is important for understanding how sound waves travel through different media. The speed of sound in a medium is influenced by its bulk modulus, which helps engineers design better acoustic materials for applications such as soundproofing and musical instruments.
Illustrative Explanation:
When designing a concert hall, acoustical engineers consider the bulk modulus of the materials used in the walls and ceiling. By selecting materials with appropriate bulk moduli, they can optimize sound quality and ensure that sound waves travel effectively throughout the space.
—
5. Factors Affecting Bulk Modulus
Several factors can influence the bulk modulus of a material:
5.1 Temperature
The bulk modulus of most materials decreases with increasing temperature. As materials heat up, they tend to expand, making them more compressible.
Illustrative Explanation:
Consider a rubber ball. When the ball is heated, it becomes softer and more pliable, resulting in a lower bulk modulus. This means that the ball will compress more easily under pressure when it is warm compared to when it is cold.
5.2 Material Composition
The composition of a material significantly affects its bulk modulus. Different materials have varying atomic structures and bonding characteristics, leading to differences in compressibility.
Illustrative Explanation:
Metals generally have higher bulk moduli than polymers. For example, steel has a bulk modulus of about 200 GPa, while rubber has a bulk modulus of around 0.01 GPa. This difference means that steel is much less compressible than rubber under the same applied pressure.
5.3 Porosity
The presence of voids or pores within a material can reduce its bulk modulus. Materials with high porosity tend to be more compressible because the air-filled spaces can collapse under pressure.
Illustrative Explanation:
Consider a sponge. When you apply pressure to a sponge, the air pockets within it compress, allowing the sponge to change shape easily. This behavior results in a lower bulk modulus compared to a solid block of material, which does not have air pockets.
—
Conclusion
The bulk modulus of elasticity is a fundamental property that plays a crucial role in understanding how materials respond to pressure. By quantifying a material’s resistance to uniform compression, the bulk modulus provides valuable insights for engineers, scientists, and researchers across various fields. From material selection and structural design to geological studies and acoustics, the bulk modulus is an essential parameter that informs our understanding of material behavior and performance. By comprehensively exploring the bulk modulus of elasticity, we gain a deeper appreciation for the complexities of materials and their applications in the world around us.