Centripetal Acceleration – Blog.Pengayaan.Com

Centripetal acceleration is a fundamental concept in physics that describes the acceleration experienced by an object moving in a circular path. This acceleration is directed toward the center of the circular path and is essential for maintaining the object’s circular motion. Understanding centripetal acceleration is crucial for analyzing various physical systems, from the motion of planets in their orbits to the behavior of vehicles navigating curves. In this comprehensive exploration of centripetal acceleration, we will delve into its definition, mathematical formulation, relationship with other physical quantities, applications, and significance in both theoretical and practical contexts.

Definition of Centripetal Acceleration

Centripetal acceleration is defined as the acceleration that acts on an object moving in a circular path, directed toward the center of the circle around which the object is moving. This acceleration is necessary to change the direction of the object’s velocity vector, allowing it to follow a curved trajectory rather than moving in a straight line. The term “centripetal” comes from the Latin words “centrum,” meaning center, and “petere,” meaning to seek, indicating that this acceleration is always directed toward the center of the circular path.

Mathematical Formulation

To mathematically express centripetal acceleration, we can start with the basic definitions of circular motion. When an object moves in a circle of radius $r$ with a constant speed $v$ , the centripetal acceleration ( $a_c$ ) can be calculated using the following formula:

$a_c = \frac{v^2}{r}$

Where:

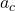$a_c$ is the centripetal acceleration (in meters per second squared, m/s²).
$v$ is the linear speed of the object (in meters per second, m/s).
$r$ is the radius of the circular path (in meters, m).

This formula indicates that the centripetal acceleration increases with the square of the speed and decreases with an increase in the radius of the circular path. Thus, for a given speed, a smaller radius results in a larger centripetal acceleration.

Relationship with Other Physical Quantities

Centripetal acceleration is closely related to several other physical quantities, including:

1. Centripetal Force: The net force required to keep an object moving in a circular path is known as centripetal force ( $F_c$ ). This force is directed toward the center of the circle and is responsible for providing the necessary centripetal acceleration. The relationship between centripetal force, mass ( $m$ ), and centripetal acceleration can be expressed as:

$F_c = m \cdot a_c$

Substituting the formula for centripetal acceleration gives:

$F_c = m \cdot \frac{v^2}{r}$

This equation shows that the centripetal force is directly proportional to the mass of the object and the square of its speed, and inversely proportional to the radius of the circular path.

2. Angular Velocity: Centripetal acceleration can also be expressed in terms of angular velocity ( $\omega$ ), which is the rate of change of angular displacement. The relationship between linear speed and angular velocity is given by:

$v = r \cdot \omega$

Substituting this into the formula for centripetal acceleration yields:

$a_c = r \cdot \omega^2$

This shows that centripetal acceleration is proportional to the radius and the square of the angular velocity.

Applications of Centripetal Acceleration

Centripetal acceleration has a wide range of applications across various fields, including:

Automotive Engineering: In automotive design, understanding centripetal acceleration is crucial for analyzing vehicle dynamics when navigating curves. Engineers must consider the centripetal force required to keep a vehicle on a curved path, which affects tire design, suspension systems, and safety features.
Astronomy: In astronomy, centripetal acceleration is essential for understanding the motion of celestial bodies, such as planets and moons, in their orbits. The gravitational force acting on these bodies provides the necessary centripetal force to maintain their circular or elliptical paths.
Sports Science: In sports, athletes often experience centripetal acceleration when running around curves or during activities such as cycling and skating. Understanding how centripetal acceleration affects performance can help in training and technique optimization.
Amusement Park Rides: Amusement park rides, such as roller coasters and merry-go-rounds, rely on centripetal acceleration to create thrilling experiences. Engineers must carefully calculate the forces involved to ensure safety while maximizing excitement.
Physics Education: Centripetal acceleration is a fundamental concept taught in physics courses. It provides students with a clear understanding of circular motion and the forces involved, enhancing their grasp of dynamics and kinematics.

Factors Influencing Centripetal Acceleration

Several factors can influence the magnitude of centripetal acceleration:

Speed: The linear speed of the object is a critical factor. As the speed increases, the centripetal acceleration increases with the square of the speed, meaning that even small increases in speed can lead to significant increases in acceleration.
Radius of the Path: The radius of the circular path also plays a crucial role. A smaller radius results in a larger centripetal acceleration for a given speed, which is why sharp turns in vehicles require more force to maintain the circular motion.
Mass of the Object: While the mass of the object does not directly affect the centripetal acceleration, it does influence the centripetal force required to maintain that acceleration. A more massive object requires a greater centripetal force to achieve the same acceleration.

Conclusion

In conclusion, centripetal acceleration is a fundamental concept in physics that describes the acceleration experienced by an object moving in a circular path. Its definition, mathematical formulation, relationship with other physical quantities, applications, and influencing factors provide a comprehensive understanding of how objects behave in circular motion. From automotive engineering and astronomy to sports science and amusement park rides, centripetal acceleration plays a critical role in shaping our understanding of motion and dynamics. As research and technology continue to evolve, the study of centripetal acceleration will remain a vital area of exploration, driving advancements in science, engineering, and everyday life. Understanding centripetal acceleration not only enhances our knowledge of physical systems but also informs practical applications that impact our daily lives and the development of new technologies.

Blog.Pengayaan.Com