A circle is a fundamental geometric shape defined as the set of all points in a plane that are equidistant from a fixed point known as the center. The distance from the center to any point on the circle is called the radius. Circles are ubiquitous in mathematics and the physical world, appearing in various contexts such as wheels, gears, and celestial bodies. Understanding the circumference of a circle is essential for applications in geometry, engineering, architecture, and many other fields. This article aims to provide an exhaustive overview of the circumference of a circle, detailing its definition, properties, formulas, and illustrative explanations for each concept.
1. Definition of Circumference
The circumference of a circle is defined as the distance around the circle. It is the perimeter or boundary length of the circle. The circumference can be thought of as the “outer edge” of the circle, and it is a crucial measurement in various applications, from calculating distances to determining material requirements for circular objects.
1.1. Key Components of a Circle
To understand the circumference, it is essential to familiarize ourselves with some key components of a circle:
- Center: The fixed point from which all points on the circle are equidistant.
- Radius (
): The distance from the center to any point on the circle. - Diameter (
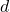): The distance across the circle, passing through the center. The diameter is twice the radius:
![\[ d = 2r \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0e5e22b96fcb73abe3263f67aceba826_l3.png "Rendered by QuickLaTeX.com")
2. Formula for Circumference
The circumference of a circle can be calculated using the following formulas:
1. Using the Radius:
![\[ C = 2\pi r \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-235adc6b21b637671e8488b8287a9dd6_l3.png "Rendered by QuickLaTeX.com")
where 
is the circumference and is the radius.
2. Using the Diameter:
![\[ C = \pi d \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a8e7ba5c461d388dff9b7f954f16695e_l3.png "Rendered by QuickLaTeX.com")
where is the diameter.
In both formulas, 
(pi) is a mathematical constant approximately equal to 
. It represents the ratio of the circumference of any circle to its diameter, making it a fundamental aspect of circular geometry.
2.1. Illustrative Explanation of the Formula
To visualize the concept of circumference, consider a circle with a radius of . The circumference can be understood as the distance you would travel if you walked around the circle once.
- Example: If we have a circle with a radius of
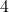cm, we can calculate the circumference using the formula:
![\[ C = 2\pi r = 2\pi(4) = 8\pi \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-85c2f281cda7a2118f64e90865398a4b_l3.png "Rendered by QuickLaTeX.com")
Using the approximate value of :
![\[ C \approx 8 \times 3.14 \approx 25.12 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8032fb5e3bba50ad36f29c50770d862a_l3.png "Rendered by QuickLaTeX.com")
This means that if you were to walk around the circle, you would cover approximately 
cm.
3. Properties of Circumference
Understanding the properties of circumference is crucial for applying the formulas effectively. Here are some key properties:
3.1. Relationship with Diameter
The circumference is directly proportional to the diameter of the circle. This relationship can be expressed as:
This means that if you know the diameter, you can easily find the circumference by multiplying by .
3.2. Constant Ratio
The ratio of the circumference to the diameter is constant for all circles, which is the value of . This property is fundamental in geometry and is used in various mathematical calculations.
3.3. Units of Measurement
The circumference is expressed in linear units, which can vary depending on the measurement system used. Common units include:
- Centimeters (cm)
- Meters (m)
- Inches (in)
- Feet (ft)
When calculating the circumference, it is essential to ensure that the radius or diameter is measured in the same unit to obtain a consistent circumference measurement.
4. Applications of Circumference
Understanding the circumference of a circle has numerous practical applications across various fields:
4.1. Engineering and Manufacturing
In engineering and manufacturing, calculating the circumference is essential for designing circular components such as gears, wheels, and pipes. Knowing the circumference helps in determining the amount of material needed for production.
- Illustrative Explanation: If an engineer is designing a circular gear with a diameter of
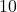cm, they can calculate the circumference to determine how much material is required for the gear’s outer edge:
![\[ C = \pi d = \pi(10) \approx 31.42 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f538f8fd6b4917b34e3e00ad1e4282e9_l3.png "Rendered by QuickLaTeX.com")
4.2. Architecture
In architecture, the circumference is used to design circular structures such as domes, columns, and arches. Understanding the circumference helps architects create aesthetically pleasing and structurally sound designs.
- Illustrative Explanation: When designing a circular fountain with a radius of
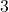meters, the architect can calculate the circumference to plan the surrounding landscaping:
![\[ C = 2\pi r = 2\pi(3) \approx 18.85 \, \text{m} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fc3eb0419404c9964d76959fbcf6245c_l3.png "Rendered by QuickLaTeX.com")
4.3. Sports and Recreation
In sports, the circumference of circular tracks and fields is crucial for determining distances and planning events. For example, running tracks are often circular, and knowing the circumference helps in measuring lap distances.
- Illustrative Explanation: A standard running track has an inner diameter of
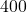meters. The circumference can be calculated to determine the distance of one lap:
![\[ C = \pi d = \pi(400) \approx 1256.64 \, \text{m} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9183435f4797238b300a47673a78decc_l3.png "Rendered by QuickLaTeX.com")
4.4. Everyday Life
In everyday life, the concept of circumference is encountered in various situations, such as measuring the length of circular objects like pizzas, plates, and wheels.
- Illustrative Explanation: If you have a pizza with a diameter of
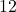inches, you can calculate the circumference to determine how much crust there is:
![\[ C = \pi d = \pi(12) \approx 37.70 \, \text{inches} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-c3c8bd1a5055216fc609c50294d673b7_l3.png "Rendered by QuickLaTeX.com")
5. Example Problems
To further illustrate the concept of calculating the circumference of a circle, let’s consider a few example problems:
Example 1: Basic Circumference Calculation
Problem: Calculate the circumference of a circle with a radius of 
cm.
Solution:
Using the formula:
![\[ C = 2\pi r = 2\pi(5) = 10\pi \approx 31.42 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7210727b5d29ac998ded708a8f018a30_l3.png "Rendered by QuickLaTeX.com")
Example 2: Circumference Using Diameter
Problem: Find the circumference of a circle with a diameter of 
meters.
Solution:
Using the formula:
![\[ C = \pi d = \pi(8) \approx 25.13 \, \text{m} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-83f64cbbc18af2b240b613663372d9ff_l3.png "Rendered by QuickLaTeX.com")
Example 3: Real-World Application
Problem: A circular garden has a radius of 
feet. How much fencing is needed to enclose the garden?
Solution:
Using the formula:
![\[ C = 2\pi r = 2\pi(6) \approx 37.70 \, \text{feet} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fdaca0fb4ac5cac6840e21b205ab5690_l3.png "Rendered by QuickLaTeX.com")
Conclusion
In conclusion, the circumference of a circle is a fundamental concept in geometry that is essential for various applications in engineering, architecture, sports, and everyday life. By understanding the components of a circle and the formulas for calculating circumference, one can effectively analyze and solve real-world problems involving circular shapes. The knowledge of circumference and its properties is a key component of our mathematical toolkit, enabling us to make informed decisions and explore the beauty of circular geometry. As we continue to delve into the vast landscape of mathematics, the understanding of the circumference of a circle will remain a foundational concept that underpins many practical applications.