Composite Functions: A Comprehensive Guide

Math
Comments

Composite functions are a fundamental concept in mathematics that arise when two or more functions are combined to create a new function. Understanding composite functions is essential for various fields, including algebra, calculus, and computer science. This article will provide a detailed exploration of composite functions, including their definition, notation, properties, examples, and illustrative explanations to enhance understanding.

1. Definition of Composite Functions

A composite function is formed when one function is applied to the result of another function. If we have two functions f and g, the composite function f \circ g (read as “f composed with g”) is defined as:

    \[ (f \circ g)(x) = f(g(x)) \]

This means that you first apply the function g to the input x, and then apply the function f to the result of g(x).

Illustrative Explanation:

Consider two functions:

  • Let f(x) = 2x + 3
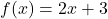
  • Let g(x) = x^2

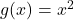
To find the composite function f \circ g, we first evaluate g(x):

    \[ g(x) = x^2 \]

Next, we substitute g(x) into f:

    \[ f(g(x)) = f(x^2) = 2(x^2) + 3 = 2x^2 + 3 \]

Thus, the composite function f \circ g is:

    \[ (f \circ g)(x) = 2x^2 + 3 \]

2. Notation of Composite Functions

The notation for composite functions is crucial for clarity. The composite function f \circ g indicates that g is applied first, followed by f. It is important to note that the order of composition matters; f \circ g is generally not the same as g \circ f.

Illustrative Explanation:

Using the previous functions f and g:

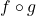  • f \circ g means we first apply 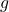g and then f.
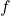  • Conversely, 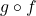g \circ f means we first apply 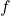f and then g.

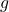Calculating g \circ f:

    \[ g(f(x)) = g(2x + 3) = (2x + 3)^2 \]

This results in a different function than f \circ g.

3. Properties of Composite Functions

Composite functions have several important properties that are useful in mathematical analysis:

A. Associativity

Composite functions are associative, meaning that if you have three functions f, g, and h, the following holds:

    \[ f \circ (g \circ h) = (f \circ g) \circ h \]

Illustrative Explanation:

Let’s consider three functions:

  • f(x) = 2x
  • g(x) = x + 1
  • h(x) = x^2

Calculating f \circ (g \circ h):

1. First, find g \circ h:

    \[ g(h(x)) = g(x^2) = x^2 + 1 \]

2. Now apply f:

    \[ f(g(h(x))) = f(x^2 + 1) = 2(x^2 + 1) = 2x^2 + 2 \]

Now, calculate (f \circ g) \circ h:

1. First, find f \circ g:

    \[ f(g(x)) = f(x + 1) = 2(x + 1) = 2x + 2 \]

2. Now apply h:

    \[ (f \circ g)(h(x)) = (2x + 2)^2 = 4x^2 + 8x + 4 \]

In this case, we see that f \circ (g \circ h) and (f \circ g) \circ h yield different results, illustrating that while composition is associative, the order of functions matters.

B. Identity Function

The identity function I(x) = x has a special property when composed with any function f:

    \[ f \circ I = f \quad \text{and} \quad I \circ f = f \]

Illustrative Explanation:

For any function f(x):

1. f \circ I(x) = f(I(x)) = f(x)
2. I \circ f(x) = I(f(x)) = f(x)

This means that composing a function with the identity function does not change the original function.

C. Distributive Property

The composite function does not distribute over addition or multiplication in the same way that multiplication distributes over addition. For example:

    \[ f \circ (g + h) \neq (f \circ g) + (f \circ h) \]

Illustrative Explanation:

Let’s consider:

  • f(x) = 2x
  • g(x) = x + 1
  • h(x) = x^2

Calculating f \circ (g + h):

1. First, find g + h:

    \[ (g + h)(x) = (x + 1) + x^2 = x^2 + x + 1 \]

2. Now apply f:

    \[ f(g + h)(x) = f(x^2 + x + 1) = 2(x^2 + x + 1) = 2x^2 + 2x + 2 \]

Now calculate (f \circ g) + (f \circ h):

1. f \circ g(x) = f(x + 1) = 2(x + 1) = 2x + 2
2. f \circ h(x) = f(x^2) = 2x^2

Adding these results:

    \[ (f \circ g)(x) + (f \circ h)(x) = (2x + 2) + (2x^2) = 2x^2 + 2x + 2 \]

In this case, we see that the results are equal, but this is not generally true for all functions.

4. Examples of Composite Functions

A. Example 1: Linear and Quadratic Functions

Let’s consider the functions:

  • f(x) = 3x + 1
  • g(x) = x^2 - 4

Calculating the composite function f \circ g:

1. First, evaluate g(x):

    \[ g(x) = x^2 - 4 \]

2. Now substitute into f:

    \[ f(g(x)) = f(x^2 - 4) = 3(x^2 - 4) + 1 = 3x^2 - 12 + 1 = 3x^2 - 11 \]

Thus, the composite function f \circ g is:

    \[ (f \circ g)(x) = 3x^2 - 11 \]

B. Example 2: Trigonometric Functions

Let’s consider the functions:

  • f(x) = \sin(x)
  • g(x) = x + \frac{\pi}{2}

Calculating the composite function f \circ g:

1. First, evaluate g(x):

    \[ g(x) = x + \frac{\pi}{2} \]

2. Now substitute into f:

    \[ f(g(x)) = f\left(x + \frac{\pi}{2}\right) = \sin\left(x + \frac{\pi}{2}\right) = \cos(x) \]

Thus, the composite function f \circ g is:

    \[ (f \circ g)(x) = \cos(x) \]

5. Conclusion

In summary, composite functions are a vital concept in mathematics that allow us to combine two or more functions to create new functions. Understanding the definition, notation, properties, and examples of composite functions is essential for analyzing and manipulating mathematical relationships. Through illustrative explanations and examples, we can appreciate the significance of composite functions in mathematical reasoning and their practical applications in various fields, including algebra, calculus, and computer science. As we continue to explore the world of mathematics, the concept of composite functions will remain central to our understanding of how functions interact, leading to deeper insights and enhanced problem-solving skills. This understanding not only enriches our mathematical knowledge but also empowers us to apply these concepts in diverse disciplines, fostering innovative solutions and insights.

Updated: December 27, 2024 — 12:29

Leave a Reply

Your email address will not be published. Required fields are marked *