In the realm of physics, forces play a crucial role in determining the motion of objects. Among these forces, conservative forces hold a special significance due to their unique properties and implications in mechanics. A conservative force is defined as a force that does work on an object in such a way that the total mechanical energy of the system remains constant. This article aims to provide an exhaustive overview of conservative forces, detailing their definition, characteristics, mathematical formulation, examples, and applications, along with illustrative explanations of each concept.
Understanding Conservative Forces
1. Definition of Conservative Force
A conservative force is a force that does not dissipate energy when it acts on an object. Instead, the work done by a conservative force depends only on the initial and final positions of the object, not on the path taken between these two points. This means that if an object moves in a closed loop under the influence of a conservative force, the total work done by the force is zero.
- Illustrative Explanation: Imagine a ball rolling down a hill and then back up to its original position. The gravitational force acting on the ball is conservative because the work done by gravity when the ball rolls down is equal to the work done against gravity when it rolls back up. The energy is conserved, and the ball returns to its original height without any loss of energy.
2. Characteristics of Conservative Forces
Conservative forces exhibit several key characteristics that distinguish them from non-conservative forces:
a. Path Independence
The work done by a conservative force is independent of the path taken by the object. It only depends on the initial and final positions of the object.
- Illustrative Explanation: Consider a hiker moving from point A to point B on a mountain. Whether the hiker takes a direct route or a winding path, the work done against gravity (a conservative force) remains the same, as it only depends on the change in height between points A and B.
b. Closed Path Work
For a conservative force, the work done in moving an object along a closed path is zero. This means that if an object returns to its starting point, the total work done by the conservative force is zero.
- Illustrative Explanation: Imagine a child pushing a toy car in a circular track. If the child pushes the car around the track and returns it to the starting point, the net work done by the force exerted on the car is zero, as the car ends up where it started.
c. Potential Energy
Conservative forces are associated with potential energy. The work done by a conservative force can be expressed in terms of the change in potential energy of the system.
- Illustrative Explanation: Think of a stretched spring. When you compress or stretch a spring, you do work on it, which is stored as potential energy. When you release the spring, this potential energy is converted back into kinetic energy as the spring returns to its equilibrium position.
3. Mathematical Formulation of Conservative Forces
The mathematical representation of conservative forces often involves the concept of potential energy. The work done by a conservative force can be expressed as:
![\[ W = -\Delta U \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-03e559ea6765ad6d1b9a765e1219e083_l3.png "Rendered by QuickLaTeX.com")
Where:
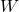is the work done by the conservative force,
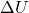is the change in potential energy of the system.
This equation indicates that the work done by a conservative force is equal to the negative change in potential energy. If the potential energy decreases, the work done is positive, indicating that energy is being converted into kinetic energy.
- Illustrative Explanation: Imagine lifting a book from the floor to a shelf. The work done against gravity (a conservative force) is equal to the increase in gravitational potential energy of the book. If you lift the book higher, it gains more potential energy, and the work done is positive.
4. Examples of Conservative Forces
Several forces in nature are classified as conservative forces. Some of the most common examples include:
a. Gravitational Force
The gravitational force is one of the most well-known conservative forces. It acts on objects with mass and is responsible for the attraction between them. The work done by gravity depends only on the change in height of the object.
- Illustrative Explanation: When you drop a ball from a height, gravity does work on the ball, converting its potential energy into kinetic energy as it falls. If you catch the ball before it hits the ground, the gravitational force has done work, but the total energy of the system remains conserved.
b. Elastic Force
The elastic force, such as that exerted by a spring, is another example of a conservative force. The work done on or by a spring is related to the displacement from its equilibrium position and can be expressed in terms of potential energy stored in the spring.
- Illustrative Explanation: When you compress a spring, you do work on it, storing energy in the form of potential energy. When you release the spring, this potential energy is converted back into kinetic energy, causing the spring to return to its original shape.
c. Electrostatic Force
The electrostatic force between charged particles is also a conservative force. The work done in moving a charge in an electric field depends only on the initial and final positions of the charge, not on the path taken.
- Illustrative Explanation: Consider two charged balloons. If you bring them closer together, the electrostatic force does work on the balloons, and the potential energy of the system changes. If you then separate them, the work done by the electrostatic force is path-independent, depending only on their initial and final positions.
5. Applications of Conservative Forces
Conservative forces have numerous applications across various fields, including:
a. Mechanical Systems
In mechanical systems, understanding conservative forces is essential for analyzing the motion of objects. Engineers and physicists use the principles of conservative forces to design systems that conserve energy, such as roller coasters and pendulums.
- Illustrative Explanation: When designing a roller coaster, engineers must consider the gravitational force acting on the cars. By ensuring that the cars have enough potential energy at the highest points, they can calculate the speeds and forces experienced by riders throughout the ride.
b. Energy Conservation
The concept of conservative forces is fundamental to the principle of conservation of energy. In closed systems where only conservative forces act, the total mechanical energy (kinetic + potential) remains constant.
- Illustrative Explanation: Imagine a swinging pendulum. At its highest point, the pendulum has maximum potential energy and minimum kinetic energy. As it swings down, potential energy is converted into kinetic energy, and at the lowest point, it has maximum kinetic energy and minimum potential energy. Throughout the swing, the total mechanical energy remains constant.
c. Astrophysics
In astrophysics, conservative forces play a crucial role in understanding the motion of celestial bodies. The gravitational force governs the orbits of planets, moons, and stars, allowing scientists to predict their movements.
- Illustrative Explanation: Consider the Earth orbiting the Sun. The gravitational force between the Earth and the Sun is a conservative force that keeps the Earth in a stable orbit. The energy of the Earth-Sun system remains conserved as the Earth moves along its elliptical path.
d. Engineering Applications
In engineering, conservative forces are considered when designing systems that involve springs, levers, and other mechanical components. Understanding how these forces work helps engineers create efficient and reliable machines.
- Illustrative Explanation: In a car’s suspension system, springs are used to absorb shocks from the road. The elastic force exerted by the springs is a conservative force that allows the car to return to its original position after hitting a bump, ensuring a smooth ride.
Conclusion
In conclusion, conservative forces are a fundamental concept in physics that describe forces that do not dissipate energy and whose work depends only on the initial and final positions of an object. By exploring their definition, characteristics, mathematical formulation, examples, and applications, we can appreciate the significance of conservative forces in understanding the behavior of mechanical systems and the conservation of energy. The study of conservative forces not only deepens our understanding of classical mechanics but also highlights their importance in various scientific and engineering applications. As research in physics continues to evolve, the principles of conservative forces will remain essential for analyzing and designing systems that rely on energy conservation and efficient motion. Understanding conservative forces is crucial for anyone interested in physics, engineering, and the natural sciences, providing a foundation for further exploration of the fascinating world of forces and energy.