An angle is formed when two rays (or line segments) share a common endpoint, known as the vertex. Angles are fundamental elements in geometry, playing a crucial role in various mathematical concepts and real-world applications, such as architecture, engineering, and art. Understanding how to construct angles accurately is essential for anyone studying geometry or involved in fields that require precise measurements. This article aims to provide an exhaustive overview of the construction of angles, detailing the definitions, methods, tools, and illustrative explanations for each concept.
1. Definition of Angles
An angle is defined as the measure of the rotation needed to bring one ray into alignment with another ray. Angles are typically measured in degrees (°) or radians. The most common types of angles include:
- Acute Angle: An angle that measures less than
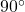. - Right Angle: An angle that measures exactly .
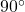- Obtuse Angle: An angle that measures more than 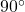but less than
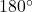. - Straight Angle: An angle that measures exactly .
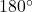- Reflex Angle: An angle that measures more than 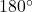but less than
.
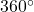1.1. Key Components of Angles
- Vertex: The common endpoint where the two rays meet.
- Sides: The two rays that form the angle.
- Angle Measure: The size of the angle, typically expressed in degrees or radians.
2. Tools for Constructing Angles
To construct angles accurately, several tools are commonly used:
2.1. Compass
A compass is a tool used to draw arcs and circles. It consists of two arms: one with a pointed end for the center and the other with a pencil or pen for drawing.
2.2. Protractor
A protractor is a semi-circular or circular tool used to measure angles in degrees. It typically has markings from 
to (or for a full protractor).
2.3. Ruler
A ruler is a straightedge used to draw straight lines and measure lengths. It is essential for creating the sides of angles.
2.4. Straightedge
A straightedge is a tool used to draw straight lines. Unlike a ruler, it does not have measurement markings.
3. Methods for Constructing Angles
There are several methods for constructing angles, each suited for different types of angles. Below, we will explore the construction of common angles: 
, 
, 
, and .
3.1. Constructing a Right Angle ()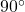
Step-by-Step Instructions:
1. Draw a Base Line: Use a ruler to draw a horizontal line segment. Label the endpoints 
and 
.
“`
A—————-B
“`
2. Place the Compass: Place the compass point on point and draw an arc that intersects the line segment 
.
3. Mark the Intersection: Label the intersection point as 
.
4. Draw an Arc: Without changing the compass width, place the compass point on point and draw an arc above the line segment .
5. Repeat for Point : Now, place the compass point on point and draw another arc that intersects the previous arc.
6. Label the Intersection: Label the intersection of the two arcs as point 
.
7. Draw the Right Angle: Use a straightedge to draw a line from point to point . The angle 
is a right angle.
Illustrative Explanation:
The construction of a right angle utilizes the property that the arcs drawn from points and are equal in radius, ensuring that the angle formed is exactly .
3.2. Constructing an Acute Angle ()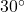
Step-by-Step Instructions:
1. Draw a Base Line: Draw a horizontal line segment .
“`
A—————-B
“`
2. Construct a Right Angle: Follow the steps above to construct a right angle at point , creating angle 
.
3. Divide the Right Angle: To create a angle, you need to bisect the right angle. Use the compass to draw an arc from point that intersects both sides of the angle.
4. Mark the Intersections: Label the intersection points as and 
.
5. Draw Arcs: With the compass set to the distance between points and , draw arcs from points and that intersect above the angle.
6. Label the Intersection: Label the intersection of the arcs as point 
.
7. Draw the Angle: Use a straightedge to draw a line from point through point . The angle 
is .
Illustrative Explanation:
By bisecting the right angle, we effectively create two equal angles of each. By further bisecting one of those angles, we achieve the desired angle.
3.3. Constructing an Obtuse Angle (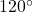
)
Step-by-Step Instructions:
1. Draw a Base Line: Draw a horizontal line segment .
“`
A—————-B
“`
2. Construct a Right Angle: Follow the steps above to construct a right angle at point , creating angle .
3. Extend the Line: Extend line segment to the right to create a new point .
4. Construct a Angle: Use the method for constructing a angle (similar to constructing a angle but starting from the right angle).
5. Draw the Angle: Use a straightedge to draw a line from point through the intersection point of the angle. The angle 
is .
Illustrative Explanation:
By constructing a angle and extending it from the right angle, we create an obtuse angle of by effectively adding to the angle formed.
3.4. Constructing a 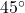Angle
Step-by-Step Instructions:
1. Draw a Base Line: Draw a horizontal line segment .
“`
A—————-B
“`
2. Construct a Right Angle: Follow the steps above to construct a right angle at point , creating angle .
3. Bisect the Right Angle: Use the compass to draw an arc from point that intersects both sides of the angle.
4. Mark the Intersections: Label the intersection points as and .
5. Draw Arcs: With the compass set to the distance between points and , draw arcs from points and that intersect above the angle.
6. Label the Intersection: Label the intersection of the arcs as point .
7. Draw the Angle: Use a straightedge to draw a line from point through point . The angle is .
Illustrative Explanation:
By bisecting the right angle, we create two equal angles of each, demonstrating the method of angle construction through bisection.
4. Applications of Angle Construction
Understanding how to construct angles accurately has numerous practical applications across various fields:
4.1. Architecture and Engineering
In architecture and engineering, constructing precise angles is crucial for ensuring structural integrity and aesthetic appeal. Accurate angles are necessary for designing buildings, bridges, and other structures.
- Illustrative Explanation: An architect may need to construct a 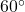angle to design a roof pitch, ensuring that the angle meets local building codes and aesthetic standards.
4.2. Art and Design
Artists and designers often use angles to create visually appealing compositions. Understanding how to construct angles accurately allows for the creation of geometric patterns and shapes.
- Illustrative Explanation: A graphic designer may need to create a logo that incorporates a 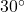angle to achieve a specific visual effect.
4.3. Mathematics Education
Teaching students how to construct angles is a fundamental part of mathematics education. It helps students develop spatial reasoning and geometric understanding.
- Illustrative Explanation: In a classroom setting, students may practice constructing various angles using a compass and protractor, reinforcing their understanding of angle relationships.
Conclusion
In conclusion, the construction of angles is a fundamental skill in geometry that has numerous applications in architecture, engineering, art, and education. By understanding the definitions, tools, and methods for constructing angles, one can effectively analyze and solve real-world problems involving angular relationships. The knowledge of angle construction is a key component of our mathematical toolkit, enabling us to create precise designs and make informed decisions in various fields. As we continue to explore the vast landscape of geometry, the ability to construct angles accurately will remain an essential skill that underpins many practical applications.