In the realm of geometry, three-dimensional shapes play a crucial role in understanding the physical world around us. Among these shapes, the cuboid and the cube are two fundamental forms that are widely studied and applied in various fields, including architecture, engineering, and design. This article aims to provide an exhaustive overview of cuboids and cubes, detailing their definitions, properties, formulas, and illustrative explanations for each concept.
1. Definition of a Cuboid
A cuboid is a three-dimensional geometric shape that has six rectangular faces, twelve edges, and eight vertices. It is also known as a rectangular prism. The faces of a cuboid can vary in size, but opposite faces are always equal in area. Cuboids can be found in everyday objects such as boxes, bricks, and rooms.
1.1. Key Components of a Cuboid
- Faces: The flat surfaces of the cuboid. A cuboid has six faces.
- Edges: The line segments where two faces meet. A cuboid has twelve edges.
- Vertices: The points where the edges meet. A cuboid has eight vertices.
- Length (
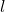 ): The measurement of one dimension of the cuboid.
): The measurement of one dimension of the cuboid. - Width (
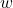 ): The measurement of the second dimension of the cuboid.
): The measurement of the second dimension of the cuboid. - Height (
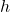 ): The measurement of the third dimension of the cuboid.
): The measurement of the third dimension of the cuboid.
1.2. Illustrative Explanation of a Cuboid
Consider a rectangular box, which is a common example of a cuboid. If we label the dimensions of the box as follows:
- Length (
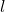 ) = 5 cm
) = 5 cm - Width (
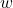 ) = 3 cm
) = 3 cm - Height (
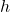 ) = 4 cm
) = 4 cm
The box has six faces: the top and bottom faces, the front and back faces, and the left and right faces. Each face is a rectangle, and opposite faces are equal in area.
2. Properties of a Cuboid
Understanding the properties of a cuboid is essential for applying geometric principles effectively. Here are some key properties:
2.1. Surface Area of a Cuboid
The surface area (![]() ) of a cuboid is the total area of all its faces. It can be calculated using the formula:
) of a cuboid is the total area of all its faces. It can be calculated using the formula:
![]()
Where:
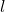 = length
= length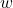 = width
= width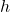 = height
= height
Example Calculation:
For our rectangular box with dimensions ![]() cm,
cm, ![]() cm, and
cm, and ![]() cm:
cm:
![]()
2.2. Volume of a Cuboid
The volume (![]() ) of a cuboid is the amount of space it occupies. It can be calculated using the formula:
) of a cuboid is the amount of space it occupies. It can be calculated using the formula:
![]()
Example Calculation:
Using the same dimensions:
![]()
This means the box can hold ![]() cubic centimeters of material.
cubic centimeters of material.
3. Definition of a Cube
A cube is a special type of cuboid where all six faces are squares of equal size. It is also known as a regular hexahedron. A cube has twelve equal edges and eight vertices, making it a highly symmetrical shape. Cubes are commonly found in everyday objects such as dice, building blocks, and storage containers.
3.1. Key Components of a Cube
- Faces: The flat surfaces of the cube. A cube has six square faces.
- Edges: The line segments where two faces meet. A cube has twelve equal edges.
- Vertices: The points where the edges meet. A cube has eight vertices.
- Side Length (
 ): The measurement of one edge of the cube.
): The measurement of one edge of the cube.
3.2. Illustrative Explanation of a Cube
Consider a standard die used in board games, which is a perfect example of a cube. If we label the side length of the die as follows:
- Side Length (
 ) = 2 cm
) = 2 cm
The die has six faces, each of which is a square measuring ![]() .
.
4. Properties of a Cube
Understanding the properties of a cube is essential for applying geometric principles effectively. Here are some key properties:
4.1. Surface Area of a Cube
The surface area (![]() ) of a cube is the total area of all its faces. It can be calculated using the formula:
) of a cube is the total area of all its faces. It can be calculated using the formula:
![]()
Where:
 = side length
= side length
Example Calculation:
For our die with a side length of ![]() cm:
cm:
![]()
4.2. Volume of a Cube
The volume (![]() ) of a cube is the amount of space it occupies. It can be calculated using the formula:
) of a cube is the amount of space it occupies. It can be calculated using the formula:
![]()
Example Calculation:
Using the same side length:
![]()
This means the die can hold ![]() cubic centimeters of material.
cubic centimeters of material.
5. Comparison Between Cuboid and Cube
While both cuboids and cubes are three-dimensional shapes, they have distinct characteristics:
| Feature | Cuboid | Cube |
|---|---|---|
| Faces | Six rectangular faces | Six square faces |
| Edges | Twelve edges of varying lengths | Twelve equal edges |
| Vertices | Eight vertices | Eight vertices |
| Surface Area | |
|
| Volume |
5.1. Illustrative Explanation of Differences
To visualize the differences, consider a shoebox (cuboid) and a standard die (cube). The shoebox has rectangular faces of different dimensions, while the die has equal square faces. This distinction affects their surface areas and volumes, as shown in the formulas above.
6. Applications of Cuboids and Cubes
Understanding cuboids and cubes has numerous practical applications across various fields:
6.1. Architecture and Construction
In architecture and construction, cuboids are often used to design buildings, rooms, and furniture. The ability to calculate surface area and volume is essential for material estimation and space planning.
- Illustrative Explanation: An architect may design a rectangular room with dimensions
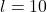 m,
m, 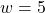 m, and
m, and 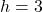 m. The surface area and volume calculations help determine the amount of paint needed for the walls and the volume of air conditioning required.
m. The surface area and volume calculations help determine the amount of paint needed for the walls and the volume of air conditioning required.
6.2. Manufacturing and Packaging
In manufacturing, cuboids and cubes are commonly used for packaging products. Understanding the dimensions and volume helps optimize storage and shipping.
- Illustrative Explanation: A company may produce boxes for shipping products. By calculating the volume of the boxes, they can determine how many products can fit in a shipping container.
6.3. Mathematics Education
Cuboids and cubes are fundamental concepts in mathematics education. They help students develop spatial reasoning and geometric understanding.
- Illustrative Explanation: In a classroom setting, students may learn about volume and surface area by constructing models of cuboids and cubes using building blocks.
Conclusion
In conclusion, cuboids and cubes are fundamental three-dimensional shapes that play a crucial role in geometry and various practical applications. By understanding their definitions, properties, and formulas, one can effectively analyze and solve real-world problems involving these shapes. The knowledge of cuboids and cubes is a key component of our mathematical toolkit, enabling us to make informed decisions in fields such as architecture, engineering, and design. As we continue to explore the vast landscape of geometry, the understanding of cuboids and cubes will remain essential for both academic and practical pursuits.