Daltons Law of Partial Pressure – Blog.Pengayaan.Com

Dalton’s Law of Partial Pressure is a fundamental principle in chemistry and physics that describes the behavior of gases in a mixture. Formulated by the English chemist John Dalton in the early 19th century, this law provides a clear understanding of how the total pressure of a gas mixture is related to the individual pressures exerted by each component gas. This article will delve into the definition, mathematical formulation, implications, applications, and illustrative explanations of Dalton’s Law of Partial Pressure, providing a thorough understanding of this essential concept.

1. Definition of Dalton’s Law of Partial Pressure

Definition: Dalton’s Law of Partial Pressure states that in a mixture of non-reacting gases, the total pressure exerted by the mixture is equal to the sum of the partial pressures of each individual gas in the mixture. Each gas in the mixture exerts pressure independently of the others, and the total pressure can be calculated by adding these individual pressures.

Mathematical Expression: The law can be mathematically expressed as:

$P_{\text{total}} = P_1 + P_2 + P_3 + \ldots + P_n$

Where:

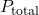$P_{\text{total}}$ is the total pressure of the gas mixture.
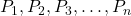$P_1, P_2, P_3, \ldots, P_n$ are the partial pressures of the individual gases in the mixture.

Illustrative Explanation: Imagine a large balloon filled with different types of colored balls (gases). Each color represents a different type of gas, and each ball exerts its own pressure against the walls of the balloon. The total pressure inside the balloon is the combined pressure from all the colored balls pushing against the walls. If you were to measure the pressure exerted by each color separately and then add them together, you would find that it equals the total pressure inside the balloon.

2. Understanding Partial Pressure

Definition of Partial Pressure: The partial pressure of a gas in a mixture is defined as the pressure that the gas would exert if it occupied the entire volume of the mixture alone at the same temperature. It reflects the contribution of that specific gas to the total pressure of the mixture.

Mathematical Expression: The partial pressure of a gas can be calculated using the ideal gas law:

$P_i = \frac{n_iRT}{V}$

Where:

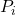$P_i$ is the partial pressure of gas $i$ .
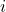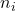$n_i$ is the number of moles of gas $i$ .
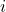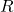$R$ is the ideal gas constant.
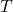$T$ is the absolute temperature in Kelvin.
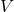$V$ is the volume of the gas mixture.

Illustrative Explanation: Continuing with the balloon analogy, if you were to take out one color of balls (one type of gas) and place them in a separate, smaller balloon, the pressure exerted by those balls in the smaller balloon would be their partial pressure. It’s as if each color of balls has its own little balloon, and the pressure they exert in their own space reflects how much they contribute to the overall pressure in the larger balloon.

3. Implications of Dalton’s Law

Dalton’s Law of Partial Pressure has several important implications in both theoretical and practical applications:

Gas Mixtures: The law allows for the analysis of gas mixtures, such as air, which is composed of nitrogen, oxygen, carbon dioxide, and other gases. Each gas contributes to the total pressure, and understanding these contributions is essential in fields like meteorology, respiratory physiology, and environmental science.
Calculating Total Pressure: Dalton’s Law simplifies the calculation of total pressure in a gas mixture. By knowing the partial pressures of individual gases, one can easily determine the total pressure without needing to know the specific interactions between the gases.
Behavior of Gases: The law is based on the assumption that gases behave ideally, meaning they do not interact with each other. While this is a good approximation under many conditions, deviations can occur at high pressures and low temperatures, where gas molecules may interact more significantly.

Illustrative Explanation: Think of a party where different groups of friends (gases) are gathered in a large room (the container). Each group is having its own conversation (exerting its own pressure), but the overall noise level (total pressure) in the room is the sum of all the conversations. If you want to know how loud the room is, you can simply ask each group how loud they are and add those levels together. However, if the groups start interacting and talking over each other, the situation becomes more complex, and the simple addition may not accurately reflect the total noise level.

4. Applications of Dalton’s Law

Dalton’s Law of Partial Pressure has numerous applications across various fields:

Respiratory Physiology: In human physiology, Dalton’s Law helps explain how gases are exchanged in the lungs. The partial pressures of oxygen and carbon dioxide in the alveoli determine the direction of gas diffusion between the blood and the air.
Chemical Reactions: In chemical reactions involving gases, Dalton’s Law can be used to predict the behavior of reactants and products in a gaseous state, allowing chemists to calculate yields and reaction rates.
Industrial Processes: In industries such as petrochemicals and pharmaceuticals, understanding the partial pressures of gases is crucial for optimizing reactions and processes, such as distillation and gas absorption.
Meteorology: Meteorologists use Dalton’s Law to understand the behavior of atmospheric gases and predict weather patterns, as the partial pressures of water vapor and other gases influence humidity and precipitation.

Illustrative Explanation: Imagine a chef (scientist) in a kitchen (laboratory) preparing a complex dish (chemical reaction). The chef needs to know how much of each ingredient (gas) to add to achieve the desired flavor (reaction outcome). By understanding how each ingredient contributes to the overall taste (total pressure), the chef can adjust the amounts accordingly. Similarly, in respiratory physiology, the body is like a chef that needs to balance the intake of oxygen and the removal of carbon dioxide to maintain a healthy “flavor” (homeostasis).

5. Example Calculation

To illustrate Dalton’s Law of Partial Pressure, let’s consider an example involving a mixture of gases:

Example: Suppose you have a container with three gases: nitrogen (N₂), oxygen (O₂), and carbon dioxide (CO₂). The partial pressures of each gas are as follows:

$P_{\text{N}_2} = 600 \, \text{mmHg}$
$P_{\text{O}_2} = 150 \, \text{mmHg}$
$P_{\text{CO}_2} = 50 \, \text{mmHg}$

1. Calculate Total Pressure:
Using Dalton’s Law, the total pressure can be calculated as:

$P_{\text{total}} = P_{\text{N}_2} + P_{\text{O}_2} + P_{\text{CO}_2}$

$P_{\text{total}} = 600 \, \text{mmHg} + 150 \, \text{mmHg} + 50 \, \text{mmHg} = 800 \, \text{mmHg}$

Illustrative Explanation: In this example, think of the container as a party where three different groups of friends (gases) are present. Each group is contributing to the overall atmosphere (total pressure) of the party. By simply adding up the contributions from each group, you can determine how lively the party is (total pressure). In this case, the total pressure of 800 mmHg reflects the combined “energy” of all three groups.

6. Conclusion

In conclusion, Dalton’s Law of Partial Pressure is a fundamental principle that describes how the total pressure of a gas mixture is the sum of the partial pressures of its individual components. This law has significant implications in various fields, including respiratory physiology, chemical reactions, industrial processes, and meteorology. By understanding the definitions, mathematical formulations, implications, applications, and illustrative explanations of Dalton’s Law, one can appreciate its importance in both theoretical and practical contexts. As we continue to explore the behavior of gases and their interactions, Dalton’s Law remains a cornerstone of our understanding of gas mixtures and their properties

Blog.Pengayaan.Com