Differentiation Formulas: A Comprehensive Exploration

Differentiation is a fundamental concept in calculus that deals with the rate at which a function changes. It is a powerful tool used to analyze and understand the behavior of functions in various fields, including physics, engineering, economics, and more. This article will explore the essential differentiation formulas, their applications, and provide illustrative explanations for each concept.

Definition of Differentiation

Differentiation is the process of finding the derivative of a function. The derivative of a function at a particular point measures the rate of change of the function’s value with respect to changes in its input value. Mathematically, if $f(x)$ is a function, the derivative is denoted as $f'(x)$ or $\frac{df}{dx}$ .

Notation

The derivative can be expressed in several notations:

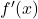$f'(x)$ (Lagrange notation)
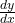$\frac{dy}{dx}$ (Leibniz notation)
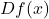$Df(x)$ (Operator notation)

Basic Differentiation Formulas

The following are some of the most fundamental differentiation formulas that serve as the building blocks for more complex differentiation tasks.

1. Power Rule

The Power Rule states that if $f(x) = x^n$ , where $n$ is a real number, then the derivative is given by:

$f'(x) = nx^{n-1}$

Illustrative Explanation

For example, if $f(x) = x^3$ :

$f'(x) = 3x^{3-1} = 3x^2$

This means that the slope of the function $x^3$ at any point $x$ is given by $3x^2$ .

2. Constant Rule

The Constant Rule states that the derivative of a constant is zero. If $c$ is a constant, then:

$\frac{d}{dx}(c) = 0$

Illustrative Explanation

For instance, if $f(x) = 5$ :

$f'(x) = 0$

This indicates that a constant function does not change, hence its rate of change (slope) is zero.

3. Constant Multiple Rule

The Constant Multiple Rule states that if $c$ is a constant and $f(x)$ is a differentiable function, then:

$\frac{d}{dx}(cf(x)) = c \cdot f'(x)$

Illustrative Explanation

For example, if $f(x) = 4x^2$ :

$\frac{d}{dx}(4x^2) = 4 \cdot \frac{d}{dx}(x^2) = 4 \cdot 2x = 8x$

This shows that the derivative of a constant multiplied by a function is simply the constant multiplied by the derivative of the function.

4. Sum Rule

The Sum Rule states that the derivative of the sum of two functions is the sum of their derivatives. If $f(x)$ and $g(x)$ are differentiable functions, then:

$\frac{d}{dx}(f(x) + g(x)) = f'(x) + g'(x)$

Illustrative Explanation

For instance, if $f(x) = x^2$ and $g(x) = x^3$ :

$\frac{d}{dx}(x^2 + x^3) = \frac{d}{dx}(x^2) + \frac{d}{dx}(x^3) = 2x + 3x^2$

This indicates that the derivative of the sum of two functions is simply the sum of their individual derivatives.

5. Difference Rule

The Difference Rule states that the derivative of the difference of two functions is the difference of their derivatives. If $f(x)$ and $g(x)$ are differentiable functions, then:

$\frac{d}{dx}(f(x) - g(x)) = f'(x) - g'(x)$

Illustrative Explanation

For example, if $f(x) = x^3$ and $g(x) = x^2$ :

$\frac{d}{dx}(x^3 - x^2) = \frac{d}{dx}(x^3) - \frac{d}{dx}(x^2) = 3x^2 - 2x$

This shows that the derivative of the difference of two functions is the difference of their derivatives.

6. Product Rule

The Product Rule states that if $f(x)$ and $g(x)$ are differentiable functions, then the derivative of their product is given by:

$\frac{d}{dx}(f(x)g(x)) = f'(x)g(x) + f(x)g'(x)$

Illustrative Explanation

For instance, if $f(x) = x^2$ and $g(x) = x^3$ :

$\frac{d}{dx}(x^2 \cdot x^3) = \frac{d}{dx}(x^2) \cdot x^3 + x^2 \cdot \frac{d}{dx}(x^3) = 2x \cdot x^3 + x^2 \cdot 3x^2 = 2x^4 + 3x^4 = 5x^4$

This indicates that the derivative of the product of two functions involves both functions and their derivatives.

7. Quotient Rule

The Quotient Rule states that if $f(x)$ and $g(x)$ are differentiable functions, then the derivative of their quotient is given by:

$\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) - f(x)g'(x)}{(g(x))^2}$

Illustrative Explanation

For example, if $f(x) = x^2$ and $g(x) = x^3$ :

$\frac{d}{dx}\left(\frac{x^2}{x^3}\right) = \frac{(2x)(x^3) - (x^2)(3x^2)}{(x^3)^2} = \frac{2x^4 - 3x^4}{x^6} = \frac{-x^4}{x^6} = -\frac{1}{x^2}$

This shows that the derivative of the quotient of two functions involves both functions and their derivatives, divided by the square of the denominator.

8. Chain Rule

The Chain Rule is used to differentiate composite functions. If $f(g(x))$ is a composite function, then the derivative is given by:

$\frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x)$

Illustrative Explanation

For example, if $f(x) = \sin(x)$ and $g(x) = x^2$ :

$\frac{d}{dx}(\sin(x^2)) = \cos(x^2) \cdot \frac{d}{dx}(x^2) = \cos(x^2) \cdot 2x$

This indicates that to differentiate a composite function, we differentiate the outer function and multiply it by the derivative of the inner function.

Higher-Order Derivatives

In addition to first derivatives, we can also find higher-order derivatives, which are derivatives of derivatives. The second derivative is denoted as $f''(x)$ or $\frac{d^2y}{dx^2}$ , and it measures the rate of change of the rate of change.

Illustrative Explanation

For example, if $f(x) = x^3$ :

The first derivative is:

$f'(x) = 3x^2$

The second derivative is:

$f''(x) = 6x$

This indicates how the slope of the function $x^3$ changes as $x$ varies.

Applications of Differentiation

Differentiation has numerous applications across various fields:

1. Physics: In physics, differentiation is used to analyze motion, where the derivative of position with respect to time gives velocity, and the derivative of velocity gives acceleration.

Illustrative Explanation

If the position of an object is given by $s(t) = t^2 + 3t$ , then the velocity is:

$v(t) = \frac{ds}{dt} = 2t + 3$

and the acceleration is:

$a(t) = \frac{dv}{dt} = 2$

2. Economics: In economics, differentiation is used to find marginal cost and marginal revenue, which are the derivatives of cost and revenue functions, respectively.

Illustrative Explanation

If the cost function is $C(x) = 5x^2 + 10x + 100$ , the marginal cost is:

$MC = \frac{dC}{dx} = 10x + 10$

3. Biology: In biology, differentiation is used to model population growth, where the rate of change of the population can be expressed as a derivative.

Illustrative Explanation

If the population $P(t)$ is modeled by $P(t) = 100e^{0.05t}$ , the growth rate is:

$\frac{dP}{dt} = 5e^{0.05t}$

4. Engineering: In engineering, differentiation is used in control systems to analyze system behavior and stability.

Illustrative Explanation

In a feedback control system, the rate of change of the output can be analyzed using derivatives to ensure system stability.

Conclusion

In conclusion, differentiation is a fundamental concept in calculus that provides powerful tools for analyzing the behavior of functions. The differentiation formulas discussed in this article, including the power rule, product rule, quotient rule, and chain rule, serve as essential building blocks for solving a wide range of problems. Understanding these formulas and their applications allows individuals to model and analyze various phenomena in fields such as physics, economics, biology, and engineering. By mastering differentiation, one gains valuable insights into the dynamic nature of functions and their rates of change, enhancing problem-solving skills and analytical thinking.

Blog.Pengayaan.Com

Differentiation Formulas: A Comprehensive Exploration

Definition of Differentiation

Notation

Basic Differentiation Formulas

1. Power Rule

Illustrative Explanation

2. Constant Rule

Illustrative Explanation

3. Constant Multiple Rule

Illustrative Explanation

4. Sum Rule

Illustrative Explanation

5. Difference Rule

Illustrative Explanation

6. Product Rule

Illustrative Explanation

7. Quotient Rule

Illustrative Explanation

8. Chain Rule

Illustrative Explanation

Higher-Order Derivatives

Illustrative Explanation

Applications of Differentiation

Illustrative Explanation

Illustrative Explanation

Illustrative Explanation

Illustrative Explanation

Conclusion

Leave a Reply Cancel reply