Understanding Drift Velocity: A Comprehensive Exploration

Drift velocity is a fundamental concept in the field of physics and electrical engineering, particularly in the study of electric currents in conductors. It describes the average velocity that charged particles, such as electrons, attain due to an electric field applied across a conductor. This article will provide an in-depth examination of drift velocity, covering its definition, mathematical formulation, factors affecting drift velocity, its significance in electrical conduction, and illustrative explanations to enhance understanding.

1. Definition of Drift Velocity

Drift velocity ( $v_d$ ) is defined as the average velocity of charged particles in a conductor when an electric field is applied. It represents the net flow of charge carriers (typically electrons in metals) in response to the electric field. While individual charge carriers move randomly due to thermal energy, the application of an electric field causes a net movement in one direction, resulting in drift velocity.

Illustrative Explanation: Imagine a crowded room filled with people (the charge carriers) moving around randomly. When someone opens a door (the electric field), a group of people starts to move toward the exit (the direction of the electric field). The average speed at which this group moves toward the exit is analogous to drift velocity.

2. Mathematical Formulation of Drift Velocity

The drift velocity can be mathematically expressed using the following formula:

$v_d = \frac{I}{nqA}$

where:

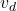$v_d$ is the drift velocity (m/s),
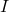$I$ is the current flowing through the conductor (A),
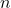$n$ is the number density of charge carriers (number of charge carriers per unit volume, m $^{-3}$ ),
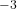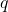$q$ is the charge of each carrier (C),
$A$ is the cross-sectional area of the conductor (m $^2$ ).

This equation shows that drift velocity is directly proportional to the current and inversely proportional to the product of the charge carrier density, charge, and cross-sectional area.

Illustrative Explanation: Think of a river (the current) flowing through a narrow channel (the conductor). The speed of the water (drift velocity) depends on how much water is flowing (current), how many fish are in the river (charge carriers), and how wide the channel is (cross-sectional area). If you increase the flow of water, the speed increases; if you narrow the channel, the speed also increases.

3. Factors Affecting Drift Velocity

Several factors influence the drift velocity of charge carriers in a conductor:

Electric Field Strength: The strength of the electric field applied across the conductor directly affects the drift velocity. A stronger electric field results in a higher drift velocity, as it exerts a greater force on the charge carriers.
Charge Carrier Density: The number density of charge carriers ( 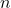$n$ ) plays a crucial role. In materials with a higher density of charge carriers, the drift velocity will be lower for a given current, as the charge carriers will collide more frequently.
Temperature: The temperature of the conductor affects the thermal motion of charge carriers. As temperature increases, the random motion of charge carriers increases, leading to more frequent collisions and a potential decrease in drift velocity for a given electric field.
Material Properties: Different materials have different intrinsic properties that affect drift velocity. For example, metals typically have higher charge carrier densities and lower resistivities compared to semiconductors, leading to different drift velocities under the same conditions.

Illustrative Explanation: Imagine a crowded highway (the conductor) where cars (charge carriers) are trying to move. If the speed limit (electric field strength) is increased, cars will go faster (higher drift velocity). If there are more cars on the road (higher charge carrier density), they will have to slow down due to traffic (more collisions). On a hot day (higher temperature), cars might be more erratic, causing delays (lower drift velocity).

4. Significance of Drift Velocity in Electrical Conduction

Drift velocity is a crucial concept in understanding how electric currents flow through conductors. Here are some key points regarding its significance:

Current Flow: Drift velocity is directly related to the flow of electric current in a conductor. Understanding drift velocity helps in analyzing how efficiently a conductor can carry current and how it responds to applied electric fields.
Resistance and Conductivity: The drift velocity is also linked to the resistance and conductivity of materials. Higher drift velocities typically indicate better conductivity, while lower drift velocities suggest higher resistance.
Device Performance: In electronic devices, drift velocity plays a role in determining the speed at which signals can propagate through circuits. Faster drift velocities can lead to improved performance in electronic components.

Illustrative Explanation: Think of drift velocity as the speed limit on a highway. If the speed limit is high (high drift velocity), cars (current) can travel quickly, leading to efficient transportation (current flow). If the speed limit is low (low drift velocity), traffic will be slower, resulting in delays (higher resistance) and potentially affecting the overall performance of the transportation system (electronic devices).

5. Drift Velocity in Different Materials

Drift velocity varies significantly across different materials, primarily due to differences in charge carrier density and mobility. Here are some examples:

Metals: In metals, such as copper and aluminum, the drift velocity is relatively high due to a high density of free electrons. These materials are excellent conductors of electricity, allowing for efficient current flow.
Semiconductors: In semiconductors, such as silicon, the drift velocity is lower than in metals due to a lower density of charge carriers. However, the drift velocity can be enhanced by doping the semiconductor with impurities, which increases the number of charge carriers.
Insulators: In insulators, such as rubber or glass, the drift velocity is negligible because there are very few free charge carriers. These materials do not conduct electricity under normal conditions.

Illustrative Explanation: Imagine different types of roads for cars. A well-paved highway (metal) allows cars to travel quickly (high drift velocity), while a gravel road (semiconductor) slows them down (lower drift velocity). A dirt path (insulator) is so rough that cars can barely move (negligible drift velocity).

6. Drift Velocity and Electric Field

The relationship between drift velocity and electric field strength can be described by the mobility ( $\mu$ ) of the charge carriers, which is defined as the drift velocity per unit electric field:

$\mu = \frac{v_d}{E}$

where:

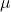$\mu$ is the mobility (m $^2$ /(V·s)),
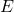$E$ is the electric field strength (V/m).

This equation shows that the drift velocity increases linearly with the electric field strength, provided that the electric field is not too strong, which could lead to non-linear effects such as saturation.

Illustrative Explanation: Think of mobility as the responsiveness of a car to the accelerator pedal (electric field). If you press the pedal lightly (low electric field), the car (charge carrier) accelerates smoothly (linear increase in drift velocity). If you press it too hard (high electric field), the car may start to skid or lose control (non-linear effects), making it harder to predict its speed.

7. Practical Applications of Drift Velocity

Understanding drift velocity is essential for various practical applications in electronics and electrical engineering:

Circuit Design: Engineers use drift velocity to design circuits that can handle specific current levels without overheating or failing. Knowing the drift velocity helps in selecting appropriate materials and dimensions for conductors.
Transistors and Diodes: In semiconductor devices like transistors and diodes, drift velocity is crucial for determining how quickly these devices can switch on and off, affecting their performance in digital circuits.
Sensors: Drift velocity is also important in the design of sensors, such as Hall effect sensors, which rely on the movement of charge carriers in response to magnetic fields.

Illustrative Explanation: Imagine a team of engineers designing a race car (circuit). They need to know how fast the car can go (drift velocity) to ensure it can handle the track (circuit conditions) without crashing (overheating or failing). They also need to consider how quickly the car can accelerate (transistors and diodes) to win the race (perform well in digital circuits).

Conclusion

Drift velocity is a fundamental concept in understanding the behavior of electric currents in conductors. By exploring its definition, mathematical formulation, factors affecting drift velocity, significance in electrical conduction, variations in different materials, and practical applications, we gain a deeper appreciation for its role in modern technology. From circuit design to semiconductor devices, drift velocity is essential for engineers and scientists working in the fields of electronics and electrical engineering. Understanding this concept not only enhances our knowledge of electrical conduction but also enables us to design and optimize systems for efficient energy transfer and signal processing.

Blog.Pengayaan.Com