Electric Field – Blog.Pengayaan.Com

The electric field is a fundamental concept in electromagnetism, representing the influence that electric charges exert on one another. It is a vector field that describes the force experienced by a positive test charge placed in the vicinity of other electric charges. Understanding electric fields is crucial for various applications in physics, engineering, and technology, including circuit design, electrostatics, and electromagnetic theory. This article aims to provide a comprehensive understanding of electric fields, including their definition, properties, mathematical representation, generation, applications, and significance in modern science and technology.

Historical Background

The concept of the electric field emerged in the 19th century as scientists sought to understand the interactions between electric charges. The groundwork for this understanding was laid by pioneers such as Charles-Augustin de Coulomb, who formulated Coulomb’s Law in the 1780s. Coulomb’s Law describes the force between two point charges and laid the foundation for the concept of the electric field.

In the early 19th century, Michael Faraday introduced the idea of the electric field as a means to visualize the forces acting at a distance between charges. Faraday’s work on electrostatics and electromagnetic induction significantly advanced the understanding of electric fields. Later, James Clerk Maxwell unified the concepts of electricity and magnetism in his famous equations, which describe how electric fields interact with magnetic fields and how they propagate as electromagnetic waves.

Definition of Electric Field

An electric field ( $\mathbf{E}$ ) is defined as the region around a charged object where other charged objects experience a force. It is a vector field, meaning it has both magnitude and direction. The electric field at a point in space is defined as the force ( $\mathbf{F}$ ) experienced by a positive test charge ( $q_0$ ) placed at that point, divided by the magnitude of the test charge:

$\mathbf{E} = \frac{\mathbf{F}}{q_0}$

Where:

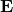$\mathbf{E}$ is the electric field vector (measured in newtons per coulomb, N/C).
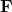$\mathbf{F}$ is the force experienced by the test charge (measured in newtons, N).
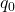$q_0$ is the magnitude of the test charge (measured in coulombs, C).

This definition implies that the electric field is independent of the test charge used to measure it, allowing for a consistent description of the electric influence in a given region.

Properties of Electric Fields

Electric fields possess several key properties that define their behavior and interactions with charges:

1. Direction: The direction of the electric field vector is defined as the direction of the force that a positive test charge would experience. Electric fields point away from positive charges and toward negative charges.

2. Magnitude: The magnitude of the electric field is proportional to the force experienced by the test charge and inversely proportional to the distance from the charge creating the field. The strength of the electric field decreases with increasing distance from the charge.

3. Superposition Principle: The total electric field at a point due to multiple charges is the vector sum of the electric fields produced by each charge individually. This principle allows for the analysis of complex charge distributions.

4. Field Lines: Electric fields can be visualized using field lines, which represent the direction and strength of the field. The density of field lines indicates the strength of the electric field, with closer lines representing stronger fields. Field lines originate from positive charges and terminate at negative charges.

5. Uniform Electric Fields: In certain configurations, such as between parallel plates with equal and opposite charges, electric fields can be uniform, meaning they have a constant magnitude and direction throughout the region.

Mathematical Representation of Electric Fields

The electric field generated by a point charge can be mathematically expressed using Coulomb’s Law. For a point charge $Q$ , the electric field ( $\mathbf{E}$ ) at a distance $r$ from the charge is given by:

$\mathbf{E} = k \frac{|Q|}{r^2} \hat{r}$

Where:

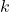$k$ is Coulomb’s constant ( $8.99 \times 10^9 \, \text{N m}^2/\text{C}^2$ ).
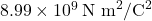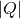$|Q|$ is the magnitude of the point charge (in coulombs).
$r$ is the distance from the charge (in meters).
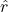$\hat{r}$ is the unit vector pointing away from the charge (for positive charges) or toward the charge (for negative charges).

For multiple point charges, the total electric field at a point can be calculated using the superposition principle:

$\mathbf{E}_{\text{total}} = \sum_{i} \mathbf{E}_i = \sum_{i} k \frac{|Q_i|}{r_i^2} \hat{r}_i$

Where $\mathbf{E}_i$ is the electric field due to the $i$ -th charge, and $r_i$ is the distance from the $i$ -th charge to the point of interest.

Generation of Electric Fields

Electric fields can be generated by various means, including:

1. Point Charges: A single point charge creates an electric field in the surrounding space, as described by Coulomb’s Law. The field strength and direction depend on the charge’s magnitude and sign.

2. Charged Conductors: When a conductor is charged, the electric field is generated in the space around it. The electric field inside a conductor in electrostatic equilibrium is zero, while the field outside the conductor is perpendicular to its surface.

3. Electric Dipoles: An electric dipole consists of two equal and opposite charges separated by a distance. The electric field generated by a dipole can be calculated using the dipole moment and is significant in molecular interactions.

4. Changing Magnetic Fields: According to Faraday’s law of electromagnetic induction, a changing magnetic field can induce an electric field. This principle is the basis for the operation of electric generators and transformers.

Applications of Electric Fields

Electric fields have numerous applications across various fields, including:

1. Electrostatics: Understanding electric fields is essential in electrostatics, which deals with stationary electric charges. Applications include electrostatic precipitators, photocopiers, and inkjet printers.

2. Capacitors: Capacitors store electrical energy in the electric field created between two conductive plates separated by an insulating material (dielectric). The behavior of capacitors is crucial in electronic circuits for energy storage and filtering.

3. Electric Field Mapping: Electric fields can be mapped using field lines to visualize the distribution of electric forces in a region. This technique is used in various scientific and engineering applications, including the design of electrical devices.

4. Medical Applications: Electric fields are used in medical technologies, such as electrocardiograms (ECGs) and electrophysiology, to monitor and analyze electrical activity in the body.

5. Particle Acceleration: Electric fields are employed in particle accelerators to accelerate charged particles to high speeds for research in particle physics and nuclear physics.

6. Electromagnetic Devices: Electric fields play a crucial role in the operation of various electromagnetic devices, including motors, generators, and transformers, which rely on the interaction between electric and magnetic fields.

Conclusion

The electric field is a fundamental concept in electromagnetism, providing a framework for understanding the interactions between electric charges. Its properties, mathematical representation, and generation mechanisms are essential for various applications in science and technology. From electrostatics to medical devices and particle accelerators, electric fields play a crucial role in shaping our understanding of the physical world and enabling technological advancements. As research in electromagnetism continues to evolve, the study of electric fields will remain integral to innovations that enhance our understanding of electricity and its applications in everyday life. Understanding electric fields not only enriches our knowledge of physics but also equips us with the tools necessary to harness their potential for future advancements in technology and science.

Blog.Pengayaan.Com