Electric flux is a fundamental concept in electromagnetism that describes the flow of electric field lines through a given surface. It is a crucial quantity in understanding electric fields, Gauss’s law, and the behavior of charged objects in electric fields. Electric flux is not only important in theoretical physics but also has practical applications in engineering, electronics, and various technologies. This article aims to provide an exhaustive overview of electric flux, including its definition, mathematical formulation, physical significance, applications, and illustrative explanations of each concept.
Definition of Electric Flux
Electric flux (![]() ) is defined as the total electric field (
) is defined as the total electric field (![]() ) passing through a given surface area (
) passing through a given surface area (![]() ). Mathematically, it is expressed as:
). Mathematically, it is expressed as:
![]()
Where:
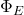 is the electric flux through the surface.
is the electric flux through the surface.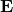 is the electric field vector.
is the electric field vector.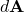 is the differential area vector, which has a magnitude equal to the area of the differential element and a direction normal to the surface.
is the differential area vector, which has a magnitude equal to the area of the differential element and a direction normal to the surface.
The dot product ![]() accounts for the angle between the electric field lines and the surface area vector, which is crucial for understanding how much of the electric field actually penetrates the surface.
accounts for the angle between the electric field lines and the surface area vector, which is crucial for understanding how much of the electric field actually penetrates the surface.
Illustrative Explanation: Imagine a flat surface placed in a uniform electric field. If the electric field lines are perpendicular to the surface, the electric flux is maximized. Conversely, if the electric field lines are parallel to the surface, the electric flux is zero because no field lines pass through the surface.
Mathematical Formulation of Electric Flux
To understand electric flux mathematically, we can break down the integral expression into simpler components. The electric flux through a flat surface can be calculated as:
![]()
Where:
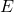 is the magnitude of the electric field.
is the magnitude of the electric field.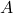 is the area of the surface.
is the area of the surface.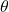 is the angle between the electric field lines and the normal to the surface.
is the angle between the electric field lines and the normal to the surface.
Illustrative Example: Consider a surface area of ![]() placed in a uniform electric field of
placed in a uniform electric field of ![]() at an angle of
at an angle of ![]() to the normal. The electric flux can be calculated as:
to the normal. The electric flux can be calculated as:
![]()
This calculation illustrates how the angle affects the amount of electric flux passing through the surface.
Physical Significance of Electric Flux
Electric flux has several important physical implications:
1. Gauss’s Law:
- Gauss’s law relates the electric flux through a closed surface to the charge enclosed within that surface. It states that the total electric flux (
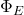 ) through a closed surface is proportional to the enclosed charge (
) through a closed surface is proportional to the enclosed charge (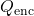 ):
):
![]()
Where ![]() is the permittivity of free space (
is the permittivity of free space (![]() ).
).
Illustrative Explanation: If you have a spherical surface surrounding a point charge, the electric flux through that surface depends only on the amount of charge inside, regardless of the size of the sphere. This principle is fundamental in electrostatics and simplifies the calculation of electric fields for symmetric charge distributions.
2. Field Strength and Surface Orientation:
- The electric flux provides insight into the strength of the electric field and the orientation of the surface. A higher electric flux indicates a stronger electric field or a surface that is more aligned with the field lines.
Illustrative Example: If you have two surfaces of equal area in the same electric field, but one is oriented perpendicular to the field lines and the other at an angle, the surface perpendicular to the field will have a greater electric flux.
3. Applications in Capacitors:
- Electric flux is also relevant in the context of capacitors, where it helps in understanding the relationship between charge, voltage, and electric field strength.
Illustrative Explanation: In a parallel plate capacitor, the electric flux between the plates is directly related to the charge stored on the plates. The greater the charge, the greater the electric flux, which in turn affects the electric field strength between the plates.
Applications of Electric Flux
Electric flux has numerous applications across various fields, including:
1. Electrostatics:
- In electrostatics, electric flux is used to analyze electric fields around charged objects and to apply Gauss’s law for calculating electric fields in symmetric charge distributions.
Illustrative Example: For a uniformly charged infinite plane sheet, the electric flux can be used to derive the electric field strength, which remains constant regardless of the distance from the sheet.
2. Electrical Engineering:
- Electric flux is crucial in the design and analysis of electrical components, such as capacitors and insulators, where understanding the electric field distribution is essential for performance and safety.
Illustrative Explanation: Engineers use electric flux calculations to ensure that capacitors can handle the electric fields generated without breaking down, which is vital for the reliability of electronic circuits.
3. Electromagnetic Theory:
- In the study of electromagnetic fields, electric flux is a key concept in understanding how electric fields interact with magnetic fields, leading to the development of Maxwell’s equations.
Illustrative Example: The displacement current term in Maxwell’s equations incorporates electric flux, allowing for the unification of electric and magnetic fields in electromagnetic wave propagation.
4. Environmental Science:
- Electric flux concepts are applied in environmental science, particularly in understanding the behavior of charged particles in the atmosphere and their interactions with electric fields.
Illustrative Explanation: Researchers study electric flux in the context of atmospheric electricity, such as lightning formation, where the movement of charged particles creates electric fields that lead to discharge events.
Conclusion
Electric flux is a fundamental concept in electromagnetism that describes the flow of electric field lines through a surface. Its mathematical formulation, physical significance, and applications in various fields highlight its importance in understanding electric fields, charge distributions, and electromagnetic interactions. By grasping the concept of electric flux, one can gain deeper insights into the behavior of electric fields and their implications in both theoretical and practical contexts. As research and technology continue to advance, the understanding of electric flux will remain crucial for innovations in electronics, engineering, and environmental science. Recognizing the significance of electric flux not only enhances our comprehension of fundamental physics but also informs the development of technologies that shape our modern world.