Equality of Matrices: A Comprehensive Guide

In the realm of linear algebra, the concept of matrix equality is fundamental to understanding how matrices interact with one another. Matrices are used extensively in various fields, including mathematics, physics, engineering, computer science, and economics. This article will provide a detailed exploration of the equality of matrices, including its definition, properties, conditions for equality, and illustrative explanations to enhance understanding.

1. Definition of Matrix Equality

Two matrices are said to be equal if they have the same dimensions and all corresponding elements are equal. This means that for two matrices $A$ and $B$ to be equal, the following conditions must be satisfied:

1. Same Dimensions: The number of rows and columns in both matrices must be identical.
2. Equal Corresponding Elements: Each element in matrix $A$ must be equal to the corresponding element in matrix $B$ .

Mathematical Notation:

If $A = [a_{ij}]$ and $B = [b_{ij}]$ , then $A = B$ if and only if:

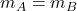$m_A = m_B$ (number of rows)
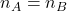$n_A = n_B$ (number of columns)
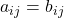$a_{ij} = b_{ij}$ for all 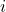$i$ and $j$

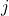
Illustrative Explanation:

Consider two matrices $A$ and $B$ :

$A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}, \quad B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$

In this case, both matrices $A$ and $B$ are $2 \times 3$ matrices (2 rows and 3 columns), and each corresponding element is equal. Therefore, we can conclude that $A = B$ .

Conversely, consider the following matrices:

$C = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad D = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$

Here, matrix $C$ is a $2 \times 2$ matrix, while matrix $D$ is a $2 \times 3$ matrix. Since their dimensions are different, we can immediately conclude that $C \neq D$ without even comparing the elements.

2. Properties of Matrix Equality

Understanding the properties of matrix equality is essential for working with matrices in various mathematical contexts. Here are some key properties:

A. Reflexive Property

Every matrix is equal to itself. This property states that for any matrix $A$ :

$A = A$

B. Symmetric Property

If matrix $A$ is equal to matrix $B$ , then matrix $B$ is equal to matrix $A$ :

$\text{If } A = B, \text{ then } B = A$

C. Transitive Property

If matrix $A$ is equal to matrix $B$ , and matrix $B$ is equal to matrix $C$ , then matrix $A$ is equal to matrix $C$ :

$\text{If } A = B \text{ and } B = C, \text{ then } A = C$

Illustrative Explanation:

Let’s consider three matrices:

$A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$

Reflexive Property: Clearly, $A = A$ .
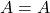Symmetric Property: Since 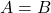$A = B$ , it follows that $B = A$ .
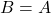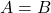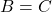Transitive Property: Since $A = B$ and $B = C$ , we can conclude that $A = C$ .

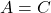3. Conditions for Matrix Equality

To determine whether two matrices are equal, we must check the following conditions:

A. Check Dimensions

First, verify that the matrices have the same dimensions. If the dimensions differ, the matrices cannot be equal.

B. Check Corresponding Elements

If the dimensions are the same, compare each corresponding element in the matrices. If all corresponding elements are equal, then the matrices are equal.

Illustrative Example:

Let’s consider two matrices:

$E = \begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix}, \quad F = \begin{bmatrix} 2 & 3 \\ 5 & 8 \end{bmatrix}$

1. Check Dimensions: Both $E$ and $F$ are $2 \times 2$ matrices, so they have the same dimensions.
2. Check Corresponding Elements:
– $e_{11} = 2$ and $f_{11} = 2$ (equal)
– $e_{12} = 3$ and $f_{12} = 3$ (equal)
– $e_{21} = 5$ and $f_{21} = 5$ (equal)
– $e_{22} = 7$ and $f_{22} = 8$ (not equal)

Since $e_{22}$ and $f_{22}$ are not equal, we conclude that $E \neq F$ .

4. Applications of Matrix Equality

Matrix equality is a foundational concept that has numerous applications across various fields:

A. Solving Systems of Linear Equations

In linear algebra, systems of equations can be represented in matrix form. When solving these systems, determining the equality of matrices is crucial for verifying solutions.

Illustrative Explanation: If you have a system of equations represented as $AX = B$ , where $A$ is the coefficient matrix, $X$ is the variable matrix, and $B$ is the constant matrix, you can find $X$ by manipulating the matrices. If you find a solution $X'$ such that $AX' = B$ , you can check the equality $B = AX'$ to verify your solution.

B. Transformations in Geometry

In geometry, matrices are used to represent transformations such as translations, rotations, and scaling. Understanding matrix equality helps in verifying that two transformations yield the same result.

Illustrative Explanation: If you have two transformation matrices $T_1$ and $T_2$ that represent the same geometric transformation, you can check if $T_1 = T_2$ to confirm that they are equivalent.

C. Computer Graphics and Image Processing

In computer graphics, matrices are used to manipulate images and perform operations such as scaling, rotating, and translating objects. Matrix equality is essential for ensuring that transformations are applied correctly.

Illustrative Explanation: When applying a series of transformations to an image, you may create a transformation matrix $T$ . If you later create another matrix $T'$ that represents the same transformation, checking if $T = T'$ ensures that the transformations are consistent.

5. Conclusion

In summary, the equality of matrices is a fundamental concept in linear algebra that involves determining whether two matrices have the same dimensions and equal corresponding elements. Understanding the conditions for matrix equality, its properties, and its applications is essential for solving problems in various fields, including mathematics, physics, engineering, and computer science. Through illustrative explanations and examples, we can appreciate the significance of matrix equality in mathematical reasoning and its practical applications in real-world scenarios. As we continue to explore the world of linear algebra, the concept of matrix equality will remain central to our understanding of mathematical relationships and transformations, ultimately contributing to advancements in technology, science, and engineering. This understanding not only enhances our mathematical knowledge but also empowers us to apply these concepts in real-world situations, leading to innovative solutions and insights across various disciplines.

Blog.Pengayaan.Com

Equality of Matrices: A Comprehensive Guide

1. Definition of Matrix Equality

Mathematical Notation:

Illustrative Explanation:

2. Properties of Matrix Equality

A. Reflexive Property

B. Symmetric Property

C. Transitive Property

Illustrative Explanation:

3. Conditions for Matrix Equality

A. Check Dimensions

B. Check Corresponding Elements

Illustrative Example:

4. Applications of Matrix Equality

A. Solving Systems of Linear Equations

B. Transformations in Geometry

C. Computer Graphics and Image Processing

5. Conclusion

Leave a Reply Cancel reply