Escape Velocity: A Comprehensive Overview

Escape velocity is a fundamental concept in physics and astrophysics that describes the minimum speed an object must reach to break free from the gravitational pull of a celestial body, such as a planet or moon, without any further propulsion. Understanding escape velocity is crucial for space exploration, satellite deployment, and understanding the dynamics of celestial bodies. This article will delve into the definition of escape velocity, the factors that influence it, the mathematical derivation, its significance in various contexts, and illustrative explanations to enhance comprehension.

What is Escape Velocity?

Definition

Escape velocity is defined as the minimum speed required for an object to escape the gravitational influence of a celestial body without any additional propulsion. It is the speed at which the kinetic energy of the object is equal to the gravitational potential energy exerted on it by the celestial body.

Illustrative Explanation: Imagine a ball thrown upwards from the surface of the Earth. If you throw it gently, it will rise for a while but eventually fall back due to gravity. However, if you throw it with enough force (at escape velocity), it will continue to rise indefinitely, breaking free from Earth’s gravitational pull.

Mathematical Expression

The escape velocity ( $v_e$ ) can be calculated using the following formula:

$v_e = \sqrt{\frac{2GM}{r}}$

where:

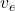$v_e$ is the escape velocity,
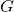$G$ is the universal gravitational constant ( $6.674 \times 10^{-11} \, \text{m}^3/\text{kg} \cdot \text{s}^2$ ),
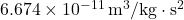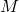$M$ is the mass of the celestial body,
$r$ is the radius of the celestial body from its center to the point of escape.
Illustrative Explanation: Think of a large rubber band stretched around a ball. The tighter the rubber band (greater mass), the more force is needed to pull the ball away from it. Similarly, the larger the mass of a celestial body, the greater the escape velocity required to overcome its gravitational pull.

Factors Influencing Escape Velocity

Several factors influence the escape velocity of a celestial body:

1. Mass of the Celestial Body

The greater the mass of the celestial body, the stronger its gravitational pull, and thus, the higher the escape velocity required.

Illustrative Explanation: Consider two balls of different sizes, one a basketball and the other a beach ball. If you want to throw both balls over a fence, you will need to throw the basketball harder because it is heavier and has more gravitational pull (in a metaphorical sense).

2. Radius of the Celestial Body

Escape velocity is inversely proportional to the radius of the celestial body. A larger radius means that the object is starting further away from the center of mass, which reduces the gravitational pull experienced at the surface.

Illustrative Explanation: Imagine standing on a tall building and trying to jump off. If you are on the ground, you need to jump higher to escape the gravitational pull of the Earth. However, if you are on the roof of a tall building, you are already higher up, so you don’t need to jump as high to escape.

3. Gravitational Constant

The universal gravitational constant ( $G$ ) is a fixed value that plays a role in determining the gravitational force between two masses. It is a fundamental constant of nature and does not change.

Illustrative Explanation: Think of 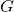$G$ as a universal rule that governs how gravity works. Just like the rules of a game dictate how players interact, 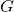$G$ dictates how masses attract each other.

Derivation of Escape Velocity

To derive the escape velocity formula, we start with the concept of energy conservation. The total mechanical energy of an object is the sum of its kinetic energy (KE) and gravitational potential energy (PE).

1. Kinetic Energy: The kinetic energy of an object with mass $m$ moving at velocity $v$ is given by:

$KE = \frac{1}{2}mv^2$

2. Gravitational Potential Energy: The gravitational potential energy of an object at a distance $r$ from the center of a celestial body with mass $M$ is given by:

$PE = -\frac{GMm}{r}$

3. Setting Up the Equation: For an object to escape the gravitational pull, the total mechanical energy must be zero or greater. Therefore, we set the kinetic energy equal to the absolute value of the gravitational potential energy:

$\frac{1}{2}mv_e^2 = \frac{GMm}{r}$

4. Solving for Escape Velocity: Canceling $m$ from both sides (assuming $m \neq 0$ ) and rearranging gives:

$v_e^2 = \frac{2GM}{r}$

Taking the square root of both sides results in the escape velocity formula:

$v_e = \sqrt{\frac{2GM}{r}}$

Illustrative Explanation: Imagine a person trying to climb a hill. The higher they climb (potential energy), the more energy they need to exert (kinetic energy) to reach the top. If they exert just enough energy to reach the top, they can escape the hill’s gravitational pull.

Significance of Escape Velocity

Escape velocity is a crucial concept in various fields, including:

1. Space Exploration

Understanding escape velocity is essential for launching spacecraft. Rockets must reach or exceed escape velocity to leave Earth’s gravitational influence and enter space.

Illustrative Explanation: Think of a rocket as a powerful slingshot. To break free from Earth’s grip, it must be launched with enough force to reach escape velocity, similar to how a slingshot must be pulled back far enough to launch a projectile into the air.

2. Satellite Deployment

Satellites must achieve a specific velocity to enter orbit around a celestial body. While this velocity is less than escape velocity, it is still significant for maintaining a stable orbit.

Illustrative Explanation: Imagine a satellite as a car driving around a circular track. To stay on the track (orbit), it must maintain a certain speed. If it goes too slow, it will fall off the track; if it goes too fast, it may break free from the track altogether.

3. Astrophysics

Escape velocity helps scientists understand the dynamics of celestial bodies, including black holes, where the escape velocity exceeds the speed of light, making it impossible for anything to escape their gravitational pull.

Illustrative Explanation: Picture a black hole as a cosmic vacuum cleaner with an incredibly strong pull. Anything that gets too close, including light, cannot escape, similar to how a vacuum cleaner pulls in everything around it.

Examples of Escape Velocity

1. Earth

The escape velocity from the surface of Earth is approximately 11.2 kilometers per second (km/s) or about 25,000 miles per hour (mph). This means that any object must reach this speed to break free from Earth’s gravitational influence.

Illustrative Explanation: Imagine a high-speed train that needs to reach a speed of 11.2 km/s to break free from the tracks and soar into the sky. If it doesn’t reach that speed, it will remain on the ground.

2. Moon

The escape velocity from the Moon is about 2.4 km/s (approximately 5,400 mph). This lower escape velocity is due to the Moon’s smaller mass and radius compared to Earth.

Illustrative Explanation: Think of the Moon as a smaller hill compared to Earth. It requires less effort (lower speed) to climb over the smaller hill than the larger one.

3. Mars

The escape velocity from Mars is approximately 5.0 km/s (about 11,200 mph). Mars has a lower escape velocity than Earth due to its smaller mass and radius.

Illustrative Explanation: Picture Mars as a medium-sized hill. It requires a moderate amount of energy (speed) to escape its gravitational pull, less than what is needed for Earth but more than what is needed for the Moon.

Conclusion

Escape velocity is a fundamental concept in physics that describes the minimum speed required for an object to break free from the gravitational pull of a celestial body. By understanding the definition, mathematical derivation, influencing factors, significance, and real-world examples of escape velocity, we gain valuable insights into the dynamics of space travel and the behavior of celestial bodies. As humanity continues to explore the cosmos, the concept of escape velocity will remain crucial in our quest to understand the universe and push the boundaries of space exploration. Whether launching satellites, sending probes to distant planets, or contemplating the mysteries of black holes, escape velocity serves as a key to unlocking the secrets of the universe.

Blog.Pengayaan.Com