In the field of statistics, data visualization plays a crucial role in understanding and interpreting data sets. One effective way to represent frequency distributions is through a frequency polygon. A frequency polygon is a graphical representation that uses line segments to connect points representing the frequencies of different categories or intervals. This article aims to provide an exhaustive overview of frequency polygons, detailing their definitions, construction methods, applications, and illustrative explanations for each concept.
1. Understanding Frequency Polygons
1.1. Definition of a Frequency Polygon
A frequency polygon is a type of graph that displays the distribution of a dataset by connecting the midpoints of each interval (or class) with straight lines. It is particularly useful for visualizing the shape of the distribution and identifying trends, patterns, and outliers in the data.
1.2. Key Components of a Frequency Polygon
- Class Intervals: The ranges of values into which the data is grouped. Each interval represents a specific range of data points.
- Frequencies: The number of occurrences of data points within each class interval.
- Midpoints: The central value of each class interval, calculated as the average of the lower and upper boundaries of the interval.
- Axes: The horizontal axis (x-axis) represents the midpoints of the class intervals, while the vertical axis (y-axis) represents the frequencies.
2. Constructing a Frequency Polygon
To construct a frequency polygon, follow these steps:
2.1. Collect and Organize Data
1. Gather Data: Collect the data you want to analyze. This could be a set of measurements, survey results, or any other quantitative data.
2. Create a Frequency Distribution Table: Organize the data into class intervals and count the number of occurrences (frequencies) in each interval.
Example of a Frequency Distribution Table
| Class Interval | Frequency |
|---|---|
| 0 – 10 | 5 |
| 11 – 20 | 8 |
| 21 – 30 | 12 |
| 31 – 40 | 10 |
| 41 – 50 | 4 |
2.2. Calculate Midpoints
3. Calculate Midpoints: For each class interval, calculate the midpoint using the formula:
![]()
Example Calculation of Midpoints
- For the interval
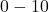 :
:
![]()
- For the interval
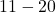 :
:
![]()
- For the interval
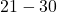 :
:
![]()
- For the interval
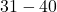 :
:
![]()
- For the interval
 :
:
![]()
2.3. Plotting the Points
4. Plot the Points: On a graph, plot the midpoints on the x-axis and the corresponding frequencies on the y-axis.
Example of Points to Plot
| Midpoint | Frequency |
|---|---|
| 5 | 5 |
| 15.5 | 8 |
| 25.5 | 12 |
| 35.5 | 10 |
| 45.5 | 4 |
2.4. Connecting the Points
5. Connect the Points: Draw straight lines between the plotted points to form the frequency polygon. It is common to also connect the last point back to the x-axis to close the polygon.
2.5. Labeling the Graph
6. Label the Graph: Add titles, labels for the axes, and any other relevant information to make the graph clear and informative.
3. Illustrative Example of a Frequency Polygon
Let’s illustrate the construction of a frequency polygon using the frequency distribution table provided earlier.
Step-by-Step Construction
- Frequency Distribution Table:
| Class Interval | Frequency |
|---|---|
| 0 – 10 | 5 |
| 11 – 20 | 8 |
| 21 – 30 | 12 |
| 31 – 40 | 10 |
| 41 – 50 | 4 |
- Calculate Midpoints:
| Class Interval | Midpoint | Frequency |
|---|---|---|
| 0 – 10 | 5 | 5 |
| 11 – 20 | 15.5 | 8 |
| 21 – 30 | 25.5 | 12 |
| 31 – 40 | 35.5 | 10 |
| 41 – 50 | 45.5 | 4 |
- Plot the Points: On a graph, plot the points (5,5)(5, 5), (15.5,8)(15.5, 8), (25.5,12)(25.5, 12), (35.5,10)(35.5, 10), and (45.5,4)(45.5, 4).
- Connect the Points: Draw straight lines between the points to form the frequency polygon.
- Label the Graph: Add a title such as “Frequency Polygon of Data Distribution” and label the x-axis as “Midpoints” and the y-axis as “Frequency”.
Visual Representation
While I cannot create visual graphics directly, you can visualize the frequency polygon as a line graph where the x-axis represents the midpoints of the class intervals and the y-axis represents the frequencies. The points plotted will create a shape that reflects the distribution of the data.
4. Applications of Frequency Polygons
Frequency polygons have several practical applications in various fields:
4.1. Data Analysis
Frequency polygons are widely used in data analysis to visualize the distribution of data sets. They help analysts identify trends, patterns, and anomalies in the data.
4.2. Comparative Analysis
When comparing multiple data sets, frequency polygons can be overlaid on the same graph. This allows for easy visual comparison of distributions, making it easier to identify differences and similarities.
4.3. Statistical Reporting
In reports and presentations, frequency polygons provide a clear and concise way to communicate statistical findings. They can effectively summarize large amounts of data in a visually appealing format.
4.4. Education
In educational settings, frequency polygons are used to teach students about data representation, statistics, and the interpretation of graphical data. They help students develop a deeper understanding of how data can be visualized and analyzed.
5. Limitations of Frequency Polygons
While frequency polygons are useful, they also have some limitations:
5.1. Loss of Information
When data is grouped into intervals, some information may be lost. For example, individual data points within an interval are not represented, which can lead to a loss of detail.
5.2. Sensitivity to Interval Width
The choice of class intervals can significantly affect the shape of the frequency polygon. Different interval widths may lead to different interpretations of the data.
5.3. Not Suitable for All Data Types
Frequency polygons are best suited for continuous data. For discrete data, other graphical representations, such as bar charts, may be more appropriate.
Conclusion
In conclusion, frequency polygons are a powerful tool for visualizing frequency distributions in statistics. By connecting the midpoints of class intervals with straight lines, frequency polygons provide a clear representation of data that helps identify trends, patterns, and outliers. While they have several applications in data analysis, reporting, and education, it is essential to be aware of their limitations, including the potential loss of information and sensitivity to interval width. As we continue to explore the vast landscape of statistics, the understanding of frequency polygons will remain a valuable skill for effectively communicating and interpreting data.