Half-Life: A Comprehensive Exploration of Its Definition, Applications, and Significance

Half-life is a fundamental concept in nuclear physics and chemistry that describes the time required for half of the radioactive nuclei in a sample to decay. This concept is crucial for understanding radioactive decay processes, the stability of isotopes, and the behavior of various materials over time. This article aims to provide an exhaustive overview of half-life, detailing its definition, mathematical representation, applications, and significance, along with illustrative explanations of each concept.

Understanding Half-Life

1. Definition of Half-Life

Half-life (denoted as $t_{1/2}$ ) is defined as the time it takes for half of the radioactive atoms in a sample to decay into a different element or isotope. This decay process is random and occurs at a characteristic rate for each radioactive isotope. The concept of half-life applies not only to radioactive decay but also to other processes, such as pharmacokinetics in medicine.

Illustrative Explanation: Imagine a large jar filled with marbles (the radioactive atoms), where half of the marbles are red (the original isotope) and the other half are blue (the decay products). The half-life is like a timer that starts when you begin removing marbles from the jar. After one half-life, you would expect to find that half of the red marbles have been removed, leaving you with an equal number of red and blue marbles. This process continues, with each half-life resulting in the removal of half of the remaining red marbles.

2. Mathematical Representation of Half-Life

The relationship between the remaining quantity of a radioactive substance and its half-life can be expressed mathematically. If $N_0$ is the initial quantity of the substance and $N$ is the quantity remaining after time $t$ , the equation can be represented as:

$N = N_0 \left( \frac{1}{2} \right)^{\frac{t}{t_{1/2}}}$

Where:

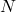$N$ = Remaining quantity of the substance
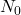$N_0$ = Initial quantity of the substance
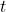$t$ = Time elapsed
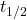$t_{1/2}$ = Half-life of the substance
Illustrative Explanation: Think of this equation as a recipe for baking a cake (the decay process). The initial quantity of cake batter (the initial quantity of the substance) is halved every time you bake a new layer (each half-life). The equation helps you predict how much cake you will have left after a certain number of layers (time elapsed).

The Decay Process

1. Radioactive Decay

Radioactive decay is a random process by which unstable atomic nuclei lose energy by emitting radiation. This decay can occur in several forms, including:

Alpha Decay: The nucleus emits an alpha particle (two protons and two neutrons), resulting in a new element with a lower atomic number.
Beta Decay: A neutron in the nucleus is transformed into a proton, emitting a beta particle (an electron or positron) and increasing the atomic number by one.
Gamma Decay: The nucleus releases energy in the form of gamma radiation without changing the number of protons or neutrons.
Illustrative Explanation: Imagine radioactive decay as a game of musical chairs (the decay process) where players (the atomic nuclei) must leave their seats (the unstable state) when the music stops (the decay event). Each type of decay represents a different way of leaving the game: some players (alpha decay) leave with a friend (the alpha particle), while others (beta decay) change their seats (transform into a different element) but stay in the game.

2. Exponential Decay

The decay of radioactive substances follows an exponential decay pattern, meaning that the rate of decay is proportional to the amount of substance remaining. This results in a characteristic curve when plotting the quantity of the substance against time.

Illustrative Explanation: Think of exponential decay as a waterfall (the decay process) where the water level (the quantity of the substance) decreases rapidly at first but slows down over time. As the water flows over the edge, the initial rush (the rapid decay) is strong, but as the level drops, the flow becomes gentler (the slowing decay), illustrating how the quantity decreases over time.

Applications of Half-Life

1. Radiometric Dating

One of the most significant applications of half-life is in radiometric dating, a technique used to determine the age of materials, such as rocks and fossils. By measuring the ratio of parent isotopes (the original radioactive material) to daughter isotopes (the decay products) and knowing the half-life of the parent isotope, scientists can calculate the age of the sample.

Illustrative Explanation: Imagine radiometric dating as a time capsule (the sample) that holds a secret (the age). By examining the contents (the isotopes) and knowing how quickly the secret is revealed (the half-life), scientists can unlock the mystery of when the time capsule was buried (the age of the material).

2. Medical Applications

In medicine, half-life is crucial for understanding the behavior of drugs in the body. The half-life of a medication determines how often it needs to be administered to maintain effective therapeutic levels. Additionally, radioactive isotopes are used in diagnostic imaging and cancer treatment, where their half-lives help determine the appropriate dosage and timing.

Illustrative Explanation: Think of the half-life of a medication as a clock (the timing) that helps patients manage their doses (the administration). Just as a clock reminds you when to take your next pill, understanding the half-life ensures that the medication remains effective in the body without causing toxicity.

3. Nuclear Power and Waste Management

In nuclear power generation, understanding the half-lives of radioactive isotopes is essential for managing nuclear fuel and waste. The half-life of isotopes in spent nuclear fuel determines how long they remain hazardous and how they should be stored or disposed of.

Illustrative Explanation: Imagine managing nuclear waste as a long-distance relay race (the process). Each runner (the isotopes) has a specific distance to cover (the half-life) before passing the baton (the waste management) to the next runner. Understanding how long each runner will take helps ensure that the race is completed safely and efficiently.

Factors Influencing Half-Life

1. Nature of the Isotope

The half-life of a radioactive isotope is intrinsic to its nuclear structure and is not influenced by external factors such as temperature, pressure, or chemical state. Each isotope has a unique half-life that can range from fractions of a second to billions of years.

Illustrative Explanation: Think of the half-life of an isotope as a unique fingerprint (the characteristic) that identifies it. Just as no two fingerprints are alike, each isotope has its own distinct half-life that defines its behavior and stability.

2. Decay Chains

Some isotopes undergo a series of decay processes, known as decay chains, where one isotope decays into another, which may also be radioactive. The half-lives of the isotopes in the decay chain can vary significantly, affecting the overall decay process.

Illustrative Explanation: Imagine a decay chain as a relay race (the process) where each runner (isotope) passes the baton (the decay) to the next runner. Each runner has their own speed (half-life), and the overall time it takes to complete the race depends on how quickly each runner can finish their leg of the race.

Conclusion

In conclusion, half-life is a fundamental concept in nuclear physics and chemistry that describes the time required for half of the radioactive nuclei in a sample to decay. From its definition and mathematical representation to its applications in radiometric dating, medicine, and nuclear power, understanding half-life is essential for grasping the behavior of radioactive materials and their implications in various fields. By appreciating the principles of half-life, we can gain insights into the processes that govern the stability and transformation of matter in our universe. As we continue to explore the complexities of radioactive decay and its applications, half-life will remain a key focus in research and education, helping us to better understand the fundamental processes that shape our world.

Blog.Pengayaan.Com