Understanding Kirchhoff’s Rules: A Comprehensive Overview

Kirchhoff’s Rules, formulated by the German physicist Gustav Kirchhoff in the mid-19th century, are fundamental principles in electrical circuit theory. These rules provide essential guidelines for analyzing complex electrical circuits, allowing engineers and scientists to understand how current and voltage behave in various configurations. This article will provide a detailed exploration of Kirchhoff’s Rules, including their definitions, applications, and illustrative explanations to enhance understanding.

1. Overview of Kirchhoff’s Rules

Kirchhoff’s Rules consist of two primary principles: Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL). Together, these rules form the foundation for circuit analysis and are widely used in electrical engineering, physics, and related fields.

A. Kirchhoff’s Current Law (KCL)

Kirchhoff’s Current Law states that the total current entering a junction (or node) in an electrical circuit must equal the total current leaving that junction. This principle is based on the conservation of electric charge, which asserts that charge cannot be created or destroyed in an isolated system.

Mathematical Representation:

$\sum I_{\text{in}} = \sum I_{\text{out}}$

Where:

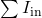$\sum I_{\text{in}}$ is the sum of currents entering the junction.
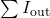$\sum I_{\text{out}}$ is the sum of currents leaving the junction.

Illustrative Explanation: Imagine a busy intersection where cars are entering and leaving. If five cars enter the intersection and three cars leave, then two cars must still be in the intersection. Similarly, in an electrical circuit, if more current enters a junction than leaves, it indicates a buildup of charge, which is not possible in a steady-state condition.

B. Kirchhoff’s Voltage Law (KVL)

Kirchhoff’s Voltage Law states that the sum of the electrical potential differences (voltages) around any closed loop in a circuit must equal zero. This principle is based on the conservation of energy, which asserts that energy supplied to a circuit must equal the energy consumed.

Mathematical Representation:

$\sum V = 0$

Where:

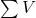$\sum V$ is the sum of all voltages in a closed loop.

Illustrative Explanation: Consider a circular track where runners start and finish at the same point. If a runner completes a lap and has run a total distance of 400 meters, they have effectively returned to their starting point, having gained no net distance. Similarly, in a closed electrical loop, the total voltage supplied by sources (like batteries) must equal the total voltage drops across components (like resistors), resulting in a net voltage of zero.

2. Applications of Kirchhoff’s Rules

Kirchhoff’s Rules are widely used in various applications, including:

A. Circuit Analysis

Engineers and technicians use Kirchhoff’s Rules to analyze complex circuits, allowing them to determine unknown currents and voltages. By applying KCL and KVL, they can set up equations that describe the behavior of the circuit.

Illustrative Explanation: Imagine a detective solving a mystery. The detective gathers clues (currents and voltages) and uses logical reasoning (Kirchhoff’s Rules) to piece together the story of what happened in the circuit. This process helps them understand how the circuit operates and identify any issues.

B. Designing Electrical Systems

When designing electrical systems, engineers use Kirchhoff’s Rules to ensure that circuits function correctly and safely. By analyzing the current and voltage distribution, they can optimize the design for efficiency and reliability.

Illustrative Explanation: Think of an architect designing a building. The architect must consider how the structure will support weight and withstand forces. Similarly, engineers use Kirchhoff’s Rules to ensure that electrical circuits can handle the flow of current and voltage without failure.

C. Troubleshooting Circuits

When troubleshooting electrical circuits, technicians apply Kirchhoff’s Rules to identify faults and malfunctions. By analyzing the current and voltage at various points in the circuit, they can pinpoint issues and make necessary repairs.

Illustrative Explanation: Imagine a mechanic diagnosing a car problem. The mechanic checks various components (like the battery, engine, and brakes) to find the source of the issue. In the same way, technicians use Kirchhoff’s Rules to check different parts of a circuit to locate faults.

3. Example Problem Using Kirchhoff’s Rules

To illustrate the application of Kirchhoff’s Rules, consider a simple circuit with two resistors and a battery:

A 12V battery is connected in series with a 4Ω resistor (R1) and a 6Ω resistor (R2).
We want to find the current flowing through the circuit.

Step 1: Apply Kirchhoff’s Voltage Law (KVL)

In a series circuit, the total voltage supplied by the battery must equal the sum of the voltage drops across the resistors. According to KVL:

$V_{\text{battery}} - V_{R1} - V_{R2} = 0$

Substituting the known values:

$12V - I \cdot 4Ω - I \cdot 6Ω = 0$

Step 2: Simplify the Equation

Combine the voltage drops:

$12V - I(4Ω + 6Ω) = 0$

$12V - 10I = 0$

Step 3: Solve for Current (I)

Rearranging the equation gives:

$10I = 12V$

$I = \frac{12V}{10Ω} = 1.2A$

Thus, the current flowing through the circuit is 1.2 amperes.

Illustrative Explanation: Think of the battery as a water pump pushing water through pipes (the resistors). The voltage from the battery represents the pressure from the pump, while the resistors represent obstacles that slow down the flow of water. By applying Kirchhoff’s Voltage Law, we can determine how much water (current) flows through the system.

4. Significance of Kirchhoff’s Rules

A. Foundation of Circuit Theory

Kirchhoff’s Rules are fundamental to understanding electrical circuits. They provide a systematic approach to analyzing complex networks, making them essential for students and professionals in electrical engineering and physics.

Illustrative Explanation: Consider the rules of grammar in a language. Just as grammar provides structure and clarity to communication, Kirchhoff’s Rules provide a framework for understanding and analyzing electrical circuits.

B. Safety and Reliability

By applying Kirchhoff’s Rules, engineers can design circuits that operate safely and reliably. Understanding current and voltage distribution helps prevent overheating, short circuits, and other electrical hazards.

Illustrative Explanation: Imagine a safety inspector checking a building for structural integrity. The inspector ensures that the building can withstand various forces and loads. Similarly, engineers use Kirchhoff’s Rules to ensure that electrical circuits can handle the flow of current and voltage without failure.

C. Advancements in Technology

Kirchhoff’s Rules have paved the way for advancements in technology, including the development of complex electronic devices, renewable energy systems, and smart grids. Understanding circuit behavior is crucial for innovation in these fields.

Illustrative Explanation: Think of a chef experimenting with new recipes. The chef needs to understand the ingredients and cooking techniques to create delicious dishes. In the same way, engineers and scientists use Kirchhoff’s Rules to innovate and develop new technologies.

5. Conclusion

In summary, Kirchhoff’s Rules are essential principles in electrical circuit theory that provide a systematic approach to analyzing current and voltage in circuits. Understanding Kirchhoff’s Current Law and Kirchhoff’s Voltage Law is crucial for anyone involved in electrical engineering, physics, or related fields. Whether you are a student, a technician, or simply curious about the world of electricity, a solid understanding of Kirchhoff’s Rules will deepen your appreciation for the intricacies of electrical systems. These rules are not just theoretical concepts; they are key tools that help us design, analyze, and innovate in the ever-evolving field of electrical engineering, making them indispensable in our increasingly electrified world.

Blog.Pengayaan.Com