The Law of Equipartition of Energy is a fundamental principle in statistical mechanics and thermodynamics that describes how energy is distributed among the various degrees of freedom of a system in thermal equilibrium. This law provides a powerful framework for understanding the behavior of gases, solids, and other physical systems at the microscopic level. By establishing a relationship between temperature and energy distribution, the equipartition theorem helps explain a wide range of phenomena in physics and chemistry. This article will explore the definition of the Law of Equipartition of Energy, its mathematical formulation, applications, implications, and illustrative examples to enhance understanding.
What is the Law of Equipartition of Energy?
Definition
The Law of Equipartition of Energy states that, at thermal equilibrium, the total energy of a system is equally distributed among its degrees of freedom. Each degree of freedom contributes an average energy of ![]() to the total energy, where
to the total energy, where ![]() is the Boltzmann constant and
is the Boltzmann constant and ![]() is the absolute temperature in Kelvin.
is the absolute temperature in Kelvin.
- Illustrative Explanation: Imagine a group of friends sharing a pizza. If there are eight slices and four friends, each friend should ideally get two slices. Similarly, in a system at thermal equilibrium, energy is distributed evenly among the available degrees of freedom, ensuring that each degree of freedom receives an equal share of energy.
Degrees of Freedom
Degrees of freedom refer to the independent ways in which a system can store energy. In classical mechanics, these can be translational, rotational, or vibrational:
1. Translational Degrees of Freedom: These correspond to the movement of particles in three-dimensional space. For a monatomic gas, there are three translational degrees of freedom (movement along the x, y, and z axes).
2. Rotational Degrees of Freedom: These correspond to the rotation of molecules around their axes. Diatomic molecules have two rotational degrees of freedom, while linear polyatomic molecules can have more.
3. Vibrational Degrees of Freedom: These correspond to the vibrational motion of atoms within a molecule. Each vibrational mode contributes two degrees of freedom (one for kinetic energy and one for potential energy).
- Illustrative Explanation: Think of a toy car. It can move forward and backward (translational), spin around its vertical axis (rotational), and its wheels can bounce up and down (vibrational). Each of these movements represents a degree of freedom, and the energy associated with each movement is distributed according to the equipartition theorem.
Mathematical Formulation
The Law of Equipartition of Energy can be mathematically expressed as follows:
![]()
where:
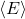 is the average energy per degree of freedom,
is the average energy per degree of freedom,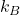 is the Boltzmann constant (
is the Boltzmann constant (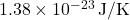 ),
),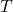 is the absolute temperature in Kelvin,
is the absolute temperature in Kelvin,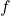 is the number of degrees of freedom.
is the number of degrees of freedom.
For example, a monatomic ideal gas has three translational degrees of freedom, leading to an average energy of:
![]()
- Illustrative Explanation: Imagine a classroom with students (degrees of freedom) and a limited number of snacks (energy). If there are three students and a total of six snacks, each student would receive two snacks. In this analogy, the snacks represent energy, and the students represent degrees of freedom, illustrating how energy is distributed evenly among them.
Applications of the Law of Equipartition of Energy
The Law of Equipartition of Energy has numerous applications across various fields of science and engineering:
1. Ideal Gases
In the study of ideal gases, the equipartition theorem helps derive the relationship between temperature and pressure. It explains why the pressure of a gas increases with temperature, as higher temperatures lead to greater average kinetic energy of the gas particles.
- Illustrative Explanation: Imagine a balloon filled with air. As you heat the balloon, the air molecules inside move faster and collide with the walls of the balloon more forcefully, increasing the pressure. The equipartition theorem quantifies this relationship between temperature and kinetic energy.
2. Heat Capacity
The equipartition theorem is used to derive the molar heat capacities of gases. For a monatomic ideal gas, the molar heat capacity at constant volume (![]() ) can be expressed as:
) can be expressed as:
![]()
where ![]() is the universal gas constant. For diatomic gases, the heat capacity increases due to additional rotational and vibrational degrees of freedom.
is the universal gas constant. For diatomic gases, the heat capacity increases due to additional rotational and vibrational degrees of freedom.
- Illustrative Explanation: Think of a pot of water on a stove. As you heat the water, the molecules gain energy and move faster, which increases the temperature of the water. The equipartition theorem helps explain how much energy is needed to raise the temperature of the water based on the degrees of freedom of the water molecules.
3. Statistical Mechanics
In statistical mechanics, the equipartition theorem provides a foundation for understanding the distribution of energy among particles in a system. It helps explain phenomena such as the Maxwell-Boltzmann distribution of molecular speeds in gases.
- Illustrative Explanation: Imagine a race where runners (particles) have different speeds. The equipartition theorem helps predict how many runners will be at each speed based on the total energy available to them, similar to how energy is distributed among particles in a gas.
4. Vibrational Modes in Solids
In solid-state physics, the equipartition theorem is used to analyze the vibrational modes of atoms in a crystal lattice. Each vibrational mode contributes to the heat capacity of the solid, helping to explain thermal properties.
- Illustrative Explanation: Picture a group of children on a trampoline. As they jump (vibrate), they store energy in their movements. The equipartition theorem helps quantify how much energy is stored in the vibrations of atoms in a solid, influencing its thermal behavior.
Implications of the Law of Equipartition of Energy
The Law of Equipartition of Energy has significant implications for our understanding of thermodynamics, statistical mechanics, and material properties:
1. Temperature and Energy Relationship
The equipartition theorem establishes a direct relationship between temperature and energy, allowing scientists to predict how systems will behave under different thermal conditions.
- Illustrative Explanation: Think of a thermostat controlling the temperature in a room. As the temperature increases, the energy in the room also increases, leading to more movement and activity. The equipartition theorem quantifies this relationship, helping us understand how energy changes with temperature.
2. Understanding Heat Transfer
The equipartition theorem aids in understanding heat transfer processes, such as conduction, convection, and radiation. It helps explain how energy is distributed among particles during these processes.
- Illustrative Explanation: Imagine a group of friends passing a ball (energy) around in a circle. As they pass the ball, everyone gets a turn to hold it, similar to how energy is distributed among particles during heat transfer.
3. Material Properties
The equipartition theorem provides insights into the thermal properties of materials, such as heat capacity and thermal conductivity. It helps engineers design materials with specific thermal characteristics for various applications.
- Illustrative Explanation: Think of a sponge that can absorb water. The amount of water it can hold (heat capacity) depends on its structure and material. The equipartition theorem helps engineers understand how different materials will respond to heat, guiding the design of effective thermal insulators or conductors.
Limitations of the Law of Equipartition of Energy
While the Law of Equipartition of Energy is a powerful tool, it has limitations:
1. Quantum Effects
At very low temperatures or in systems with quantized energy levels, the equipartition theorem may not hold. Quantum mechanics introduces additional complexities that can alter energy distribution.
- Illustrative Explanation: Imagine a game where players can only move in specific steps (quantized energy levels). In this case, the equipartition theorem may not accurately predict how energy is distributed, as players cannot freely share energy like in classical systems.
2. Non-Ideal Systems
The equipartition theorem is based on the assumption of ideal systems. In real-world scenarios, interactions between particles, non-conservative forces, and other factors can lead to deviations from the expected energy distribution.
- Illustrative Explanation: Think of a crowded dance floor where people bump into each other (interactions). The equipartition theorem assumes everyone can move freely, but in reality, interactions can disrupt the smooth distribution of energy.
Conclusion
The Law of Equipartition of Energy is a fundamental principle that describes how energy is distributed among the degrees of freedom of a system in thermal equilibrium. By establishing a relationship between temperature and energy, the equipartition theorem provides valuable insights into the behavior of gases, solids, and other physical systems. Its applications span various fields, including thermodynamics, statistical mechanics, and material science, helping us understand heat transfer, temperature relationships, and material properties. While the equipartition theorem has limitations, particularly in quantum and non-ideal systems, it remains a cornerstone of classical physics. Understanding this law is essential for grasping the intricate connections between energy, temperature, and the behavior of matter, paving the way for advancements in science and technology. The equipartition theorem is not just a theoretical concept; it is a vital tool for exploring the fundamental nature of energy and its role in the universe.