An LCR circuit, also known as an RLC circuit, is an electrical circuit that consists of three fundamental components: an inductor (L), a capacitor (C), and a resistor (R). These circuits are essential in the study of electrical engineering and physics, as they exhibit unique behaviors in response to alternating current (AC) and direct current (DC) signals. LCR circuits are widely used in various applications, including filters, oscillators, and tuning circuits. This article aims to provide an exhaustive overview of LCR circuits, detailing their components, behavior, analysis, and applications, along with illustrative explanations of each concept.
Understanding the Components of an LCR Circuit
1. Inductor (L)
An inductor is a passive electrical component that stores energy in a magnetic field when an electric current flows through it. The inductance (L) is measured in henries (H) and is defined as the ratio of the induced electromotive force (EMF) to the rate of change of current.
- Illustrative Explanation: Imagine a coil of wire wrapped around a core. When you pass current through the coil, it creates a magnetic field around it, similar to how a magnet creates a field. If you try to change the current quickly, the inductor resists this change, storing energy in the magnetic field.
2. Capacitor (C)
A capacitor is another passive component that stores energy in an electric field. It consists of two conductive plates separated by an insulating material (dielectric). The capacitance (C) is measured in farads (F) and is defined as the amount of charge stored per unit voltage.
- Illustrative Explanation: Think of a capacitor as a water tank. When you fill the tank (apply voltage), it stores water (charge). The amount of water it can hold depends on the size of the tank (capacitance) and the pressure (voltage) applied. When you open the tap (discharge), the water flows out, similar to how charge flows from a capacitor.
3. Resistor (R)
A resistor is a passive component that opposes the flow of electric current, converting electrical energy into heat. The resistance (R) is measured in ohms (Ω) and is defined as the ratio of voltage across the resistor to the current flowing through it.
- Illustrative Explanation: Imagine a narrow pipe through which water flows. The narrower the pipe (higher resistance), the harder it is for water to flow through. Similarly, a resistor limits the flow of electric current in a circuit.
Behavior of LCR Circuits
4. Types of LCR Circuits
LCR circuits can be classified into two main types based on their configuration:
a. Series LCR Circuit
In a series LCR circuit, the inductor, capacitor, and resistor are connected in a single path, meaning the same current flows through all components. The total impedance (Z) of the circuit is the sum of the individual impedances of the components.
- Illustrative Explanation: Picture a train with three cars (the inductor, capacitor, and resistor) connected in a line. The same number of passengers (current) travels through each car, and the total resistance to movement (impedance) is the sum of the resistance of each car.
b. Parallel LCR Circuit
In a parallel LCR circuit, the inductor, capacitor, and resistor are connected across the same voltage source, meaning the voltage across each component is the same. The total impedance is calculated using the reciprocal of the sum of the reciprocals of the individual impedances.
- Illustrative Explanation: Imagine three water tanks (the inductor, capacitor, and resistor) connected to a single water source. Each tank fills up independently, but they all experience the same water pressure (voltage). The total flow rate (current) is the sum of the flow rates through each tank.
5. Impedance in LCR Circuits
Impedance (Z) is a measure of how much a circuit resists the flow of alternating current (AC). It combines both resistance (R) and reactance (X), which is the opposition to current flow due to inductance and capacitance. The total impedance in a series LCR circuit is given by:
![\[ Z = \sqrt{R^2 + (X_L - X_C)^2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b866aae1437325dccc24d5f5572bfeb9_l3.png "Rendered by QuickLaTeX.com")
Where:
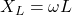(inductive reactance),
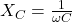(capacitive reactance),
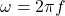(angular frequency).- Illustrative Explanation: Think of impedance as the total resistance to water flow in a complex plumbing system. The resistance from the pipes (R) and the resistance from the bends and turns (reactance) combine to determine how easily water (current) can flow through the system.
6. Resonance in LCR Circuits
Resonance occurs in LCR circuits when the inductive reactance equals the capacitive reactance (
). At this point, the circuit can oscillate at its natural frequency, known as the resonant frequency (
), which is given by:
![\[ f_0 = \frac{1}{2\pi\sqrt{LC}} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-3f62f3da3dab2303c8873bbc3314aabb_l3.png "Rendered by QuickLaTeX.com")
At resonance, the impedance is minimized, and the circuit can draw maximum current from the source.
- Illustrative Explanation: Imagine a swing at a playground. When you push the swing at just the right moment (resonance), it goes higher and higher. Similarly, in an LCR circuit, when the frequency of the AC source matches the natural frequency of the circuit, the current oscillates with maximum amplitude.
Analysis of LCR Circuits
7. AC Analysis of LCR Circuits
When analyzing LCR circuits with alternating current (AC), the behavior of the circuit can be described using phasors, which represent sinusoidal voltages and currents as rotating vectors. The voltage and current can be expressed in terms of their magnitudes and phase angles.
- Illustrative Explanation: Picture a rotating wheel. The position of a point on the wheel represents the instantaneous value of voltage or current. As the wheel rotates, the point moves up and down, creating a sinusoidal wave. Phasors simplify the analysis by allowing us to work with the magnitudes and angles instead of the time-varying functions.
8. Time Response of LCR Circuits
The time response of an LCR circuit can be analyzed using differential equations. The behavior of the circuit can be classified into two categories:
a. Transient Response
The transient response describes how the circuit behaves when a voltage is suddenly applied or removed. It involves the charging and discharging of the capacitor and the current changes in the inductor.
- Illustrative Explanation: Imagine turning on a water pump suddenly. Initially, the water flow (current) takes time to stabilize as the pipes fill up (capacitor charging). The transient response captures this initial behavior before the system reaches a steady state.
b. Steady-State Response
The steady-state response describes the behavior of the circuit after the transient effects have dissipated. In this state, the circuit operates under continuous AC conditions, and the voltages and currents are sinusoidal.
- Illustrative Explanation: Continuing with the water pump analogy, once the pipes are full and the flow stabilizes, the system reaches a steady state where the water flows consistently, similar to how the circuit operates under continuous AC conditions.
Applications of LCR Circuits
9. Filters
LCR circuits are commonly used in electronic filters to allow certain frequencies to pass while blocking others. They can be configured as low-pass, high-pass, band-pass, or band-stop filters.
- Illustrative Explanation: Think of a coffee filter that allows liquid coffee to pass through while trapping coffee grounds. Similarly, an LCR filter allows specific frequencies to pass while blocking unwanted frequencies.
10. Oscillators
LCR circuits are used in oscillators to generate oscillating signals, such as sine waves or square waves. These circuits are essential in radio transmitters and receivers.
- Illustrative Explanation: Imagine a swing that keeps going back and forth after being pushed. An LCR oscillator generates oscillating signals, similar to how the swing continues to move after an initial push.
11. Tuning Circuits
LCR circuits are used in tuning circuits to select specific frequencies in radios and televisions. By adjusting the values of L and C, the circuit can be tuned to resonate at the desired frequency.
- Illustrative Explanation: Think of a radio dial that allows you to select different stations. By tuning the LCR circuit, you can adjust the frequency to match the desired radio station, just like turning the dial to find the right frequency.
12. Power Factor Correction
LCR circuits are used in power factor correction to improve the efficiency of electrical systems. By adding capacitors or inductors, the circuit can adjust the phase relationship between voltage and current, reducing losses in power systems.
- Illustrative Explanation: Imagine a team of rowers in a boat. If they all row in sync (correct power factor), the boat moves efficiently. If they row out of sync (poor power factor), the boat moves slower and wastes energy. LCR circuits help synchronize the voltage and current for better efficiency.
Conclusion
In conclusion, LCR circuits are fundamental electrical circuits that consist of inductors, capacitors, and resistors. By understanding their components, behavior, analysis, and applications, we can appreciate the significance of LCR circuits in various fields, including electronics, telecommunications, and power systems. From filtering and oscillation to tuning and power factor correction, LCR circuits play a crucial role in modern technology. As advancements in electrical engineering continue, the study of LCR circuits will remain essential for developing innovative solutions and enhancing our understanding of electrical systems.