Moment of Inertia of Rigid Bodies: Definition, Properties, Calculation, and Applications

The moment of inertia (often denoted as $I$ ) is a fundamental concept in physics and engineering that quantifies the rotational inertia of a rigid body. It describes how difficult it is to change the rotational motion of an object about a given axis. The moment of inertia depends not only on the mass of the object but also on the distribution of that mass relative to the axis of rotation. This article aims to provide an exhaustive overview of the moment of inertia of rigid bodies, detailing its definition, properties, calculation methods, and applications, along with illustrative explanations of each concept.

Understanding Moment of Inertia

1. Definition of Moment of Inertia

The moment of inertia of a rigid body is defined as the sum of the products of the mass of each particle in the body and the square of its distance from the axis of rotation. Mathematically, it can be expressed as:

$I = \sum m_i r_i^2$

Where:

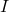$I$ is the moment of inertia,
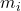$m_i$ is the mass of the 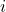$i$ -th particle,
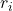$r_i$ is the distance of the 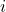$i$ -th particle from the axis of rotation.

For continuous bodies, the moment of inertia can be calculated using an integral:

$I = \int r^2 \, dm$

Where $dm$ is an infinitesimal mass element.

Illustrative Explanation: Imagine a spinning figure skater (the rigid body) who pulls in their arms to spin faster. The moment of inertia is like a measure of how spread out their mass is from the center of rotation. When the skater pulls their arms in (reducing the distance of their mass from the axis), their moment of inertia decreases, allowing them to spin faster. Just as the skater’s position affects their spin, the distribution of mass in a rigid body influences its moment of inertia.

Properties of Moment of Inertia

The moment of inertia has several key properties that influence the rotational dynamics of rigid bodies.

1. Dependence on Axis of Rotation

The moment of inertia varies depending on the axis about which the body is rotating. Different axes can lead to different moments of inertia for the same object.

Illustrative Explanation: Consider a solid disk (the rigid body) rotating about its central axis versus rotating about an edge. When the disk spins around its center, it has a certain moment of inertia. However, if it rotates around the edge, the mass is distributed further from the axis, resulting in a larger moment of inertia. Just as the axis of rotation changes the dynamics of the spinning disk, the moment of inertia is sensitive to the choice of axis.

2. Additivity of Moment of Inertia

The moment of inertia of a composite body can be calculated by summing the moments of inertia of its individual components about the same axis. This property allows for the analysis of complex shapes by breaking them down into simpler parts.

Illustrative Explanation: Imagine a seesaw (the composite body) made up of two planks (the components) attached at a pivot point. To find the total moment of inertia of the seesaw, you can calculate the moment of inertia of each plank about the pivot and then add them together. Just as the total weight of the seesaw is the sum of the weights of the planks, the total moment of inertia is the sum of the individual moments.

3. Parallel Axis Theorem

The parallel axis theorem states that the moment of inertia of a body about any axis parallel to an axis through its center of mass can be calculated using the formula:

$I = I_{cm} + Md^2$

Where:

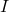$I$ is the moment of inertia about the new axis,
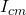$I_{cm}$ is the moment of inertia about the center of mass axis,
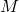$M$ is the total mass of the body,
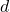$d$ is the distance between the two axes.
Illustrative Explanation: Picture a rectangular beam (the rigid body) with its center of mass at the midpoint. If you want to find the moment of inertia about one end of the beam, you can use the parallel axis theorem. By knowing the moment of inertia about the center and the distance to the end, you can easily calculate the moment of inertia about the end. Just as the theorem simplifies the calculation of the seesaw’s moment of inertia, it provides a powerful tool for analyzing various rigid bodies.

Calculation of Moment of Inertia

Calculating the moment of inertia involves different methods depending on the shape and mass distribution of the rigid body.

1. For Simple Geometric Shapes

For common geometric shapes, the moment of inertia can be calculated using standard formulas. Here are a few examples:

Solid Cylinder (about its central axis):

$I = \frac{1}{2} M R^2$

Where $M$ is the mass and $R$ is the radius.

Solid Sphere (about its central axis):

$I = \frac{2}{5} M R^2$

Rectangular Plate (about an axis through its center and parallel to one side):

$I = \frac{1}{12} M (b^2 + h^2)$

Where $b$ is the base and $h$ is the height.

Illustrative Explanation: Imagine a solid cylinder (the rigid body) like a can of soup. To find its moment of inertia about its central axis, you can use the formula 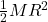$\frac{1}{2} M R^2$ . Just as the formula provides a quick way to calculate the can’s rotational inertia, these standard formulas simplify the process for various shapes.

2. For Composite Bodies

For composite bodies, the moment of inertia can be calculated by breaking the body into simpler shapes, calculating the moment of inertia for each shape, and then summing them up.

Illustrative Explanation: Picture a toy consisting of a solid cube and a solid cylinder glued together (the composite body). To find the total moment of inertia, you can calculate the moment of inertia for the cube and the cylinder separately and then add them together. Just as combining the weights of the two toys gives you the total weight, summing the moments of inertia provides the total rotational inertia.

3. Using Integration for Irregular Shapes

For irregularly shaped bodies, the moment of inertia can be calculated using calculus. The integral form allows for the calculation of the moment of inertia by integrating over the entire volume of the body.

Illustrative Explanation: Imagine a complex sculpture (the irregular shape) made of clay. To find its moment of inertia, you can think of slicing the sculpture into tiny pieces (the infinitesimal mass elements) and calculating the moment of inertia for each piece. By integrating these contributions over the entire volume, you can determine the total moment of inertia. Just as slicing the sculpture helps you understand its structure, integration provides a method to analyze the moment of inertia of complex shapes.

Applications of Moment of Inertia

The moment of inertia has numerous applications across various fields, including engineering, physics, and biomechanics.

1. Rotational Dynamics

In rotational dynamics, the moment of inertia plays a crucial role in determining the angular acceleration of an object when subjected to a torque. According to Newton’s second law for rotation, the relationship can be expressed as:

$\tau = I \alpha$

Where:

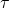$\tau$ is the torque,
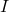$I$ is the moment of inertia,
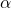$\alpha$ is the angular acceleration.
Illustrative Explanation: Imagine a merry-go-round (the rigid body) being pushed by a child (the torque). The moment of inertia determines how quickly the merry-go-round will spin. If the child applies a certain amount of force (torque), the moment of inertia tells us how fast the merry-go-round will accelerate. Just as the child’s push influences the spin, the moment of inertia is critical in understanding rotational motion.

2. Mechanical Engineering

In mechanical engineering, the moment of inertia is essential for designing rotating machinery, such as flywheels, gears, and turbines. Engineers must consider the moment of inertia to ensure that these components can withstand the forces and torques they will encounter during operation.

Illustrative Explanation: Picture a flywheel (the rotating component) in a car engine. The moment of inertia of the flywheel affects how smoothly the engine runs and how quickly it can accelerate. Engineers must calculate the moment of inertia to design a flywheel that balances performance and efficiency. Just as the flywheel’s design impacts the engine’s operation, the moment of inertia is vital in mechanical systems.

3. Structural Analysis

In structural engineering, the moment of inertia is used to analyze the bending and torsional stiffness of beams and other structural elements. A higher moment of inertia indicates greater resistance to bending, which is crucial for ensuring the safety and stability of structures.

Illustrative Explanation: Imagine a long beam (the structural element) supporting a heavy load (the weight). The moment of inertia determines how much the beam will bend under the load. If the moment of inertia is high, the beam will resist bending and remain stable. Just as the beam’s design affects its ability to support weight, the moment of inertia is critical in structural analysis.

4. Biomechanics

In biomechanics, the moment of inertia is important for understanding human movement and the mechanics of the body. It helps analyze how different body segments contribute to overall motion during activities such as running, jumping, and throwing.

Illustrative Explanation: Picture a basketball player (the human body) preparing to jump. The moment of inertia of their arms and legs affects how quickly they can rotate their body in the air. By understanding the moment of inertia, coaches can help athletes optimize their movements for better performance. Just as the player’s technique influences their jump, the moment of inertia is essential in biomechanics.

Conclusion

In conclusion, the moment of inertia of rigid bodies is a fundamental concept that plays a crucial role in understanding rotational dynamics, mechanical systems, structural analysis, and biomechanics. By exploring its definition, properties, calculation methods, and applications, we can appreciate the significance of the moment of inertia in various fields, including engineering, physics, and sports science. As technology continues to advance, the role of the moment of inertia will remain vital, contributing to innovations in design, analysis, and performance optimization. The study of moment of inertia not only deepens our understanding of rotational motion but also highlights the intricate relationship between mass distribution and dynamic behavior in our world. Understanding the moment of inertia is essential for optimizing performance, ensuring safety, and enhancing the functionality of systems in a wide range of applications.

Blog.Pengayaan.Com

Moment of Inertia of Rigid Bodies: Definition, Properties, Calculation, and Applications

Understanding Moment of Inertia

1. Definition of Moment of Inertia

Properties of Moment of Inertia

1. Dependence on Axis of Rotation

2. Additivity of Moment of Inertia

3. Parallel Axis Theorem

Calculation of Moment of Inertia

1. For Simple Geometric Shapes

2. For Composite Bodies

3. Using Integration for Irregular Shapes

Applications of Moment of Inertia

1. Rotational Dynamics

2. Mechanical Engineering

3. Structural Analysis

4. Biomechanics

Conclusion

Leave a Reply Cancel reply