The concept of the multiplicative inverse is a fundamental idea in mathematics, particularly in algebra and number theory. The multiplicative inverse of a number is the value that, when multiplied by the original number, yields the identity element for multiplication, which is ![]() . This concept is crucial in various mathematical operations, including solving equations, working with fractions, and understanding functions. This article aims to provide an exhaustive overview of the multiplicative inverse, detailing its definition, properties, applications, and illustrative explanations for each concept.
. This concept is crucial in various mathematical operations, including solving equations, working with fractions, and understanding functions. This article aims to provide an exhaustive overview of the multiplicative inverse, detailing its definition, properties, applications, and illustrative explanations for each concept.
1. Definition of the Multiplicative Inverse
The multiplicative inverse of a number ![]() is defined as the number
is defined as the number ![]() such that:
such that:
![]()
In other words, if ![]() is a non-zero number, its multiplicative inverse is given by:
is a non-zero number, its multiplicative inverse is given by:
![]()
This means that multiplying a number by its multiplicative inverse results in the multiplicative identity, which is ![]() .
.
- Illustrative Explanation: Consider the number
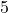 . The multiplicative inverse of
. The multiplicative inverse of 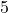 is
is 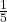 because:
because:
![]()
Similarly, for the number ![]() , the multiplicative inverse is
, the multiplicative inverse is ![]() :
:
![]()
It is important to note that the multiplicative inverse is not defined for ![]() because there is no number that can be multiplied by
because there is no number that can be multiplied by ![]() to yield
to yield ![]() .
.
2. Properties of the Multiplicative Inverse
The multiplicative inverse has several important properties that are useful in various mathematical contexts:
2.1. Existence of the Inverse
The multiplicative inverse exists for all non-zero real numbers. For any non-zero number ![]() , there is a unique multiplicative inverse
, there is a unique multiplicative inverse ![]() .
.
- Illustrative Explanation: If you take any non-zero number, such as
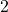 , its multiplicative inverse is
, its multiplicative inverse is 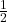 . This holds true for any non-zero number, whether it is positive or negative.
. This holds true for any non-zero number, whether it is positive or negative.
2.2. Multiplicative Identity
The product of a number and its multiplicative inverse is always equal to ![]() :
:
![]()
- Illustrative Explanation: If you have
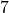 , then:
, then:
![]()
This property is fundamental in algebra, particularly when simplifying expressions or solving equations.
2.3. Multiplicative Inverse of a Fraction
For a fraction ![]() (where
(where ![]() ), the multiplicative inverse is given by:
), the multiplicative inverse is given by:
![]()
- Illustrative Explanation: If you have the fraction
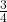 , its multiplicative inverse is
, its multiplicative inverse is 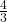 :
:
![]()
This property is particularly useful when working with fractions in algebraic expressions.
2.4. Multiplicative Inverse of a Product
The multiplicative inverse of a product of two numbers is the product of their multiplicative inverses:
![]()
- Illustrative Explanation: If you take
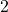 and
and 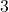 , the multiplicative inverse of their product
, the multiplicative inverse of their product 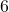 is:
is:
![]()
This property is useful in simplifying complex expressions involving products.
2.5. Multiplicative Inverse in Algebraic Structures
In algebraic structures such as fields and groups, the multiplicative inverse is a crucial concept. In a field, every non-zero element has a multiplicative inverse, which allows for division.
- Illustrative Explanation: In the field of rational numbers, every non-zero rational number has a multiplicative inverse. For example, the multiplicative inverse of
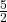 is
is 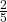 :
:
![]()
3. Applications of the Multiplicative Inverse
The multiplicative inverse has various applications across different fields:
3.1. Solving Equations
The multiplicative inverse is often used to solve equations, particularly linear equations. When an equation involves multiplication by a variable, the multiplicative inverse can be used to isolate the variable.
- Illustrative Explanation: Consider the equation
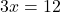 . To solve for
. To solve for 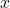 , you can multiply both sides by the multiplicative inverse of
, you can multiply both sides by the multiplicative inverse of 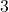 :
:
![]()
3.2. Working with Fractions
When performing operations with fractions, the multiplicative inverse is essential for division. Dividing by a fraction is equivalent to multiplying by its multiplicative inverse.
- Illustrative Explanation: If you want to divide
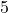 by
by 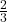 , you can multiply by the multiplicative inverse:
, you can multiply by the multiplicative inverse:
![]()
3.3. Matrix Inversion
In linear algebra, the concept of the multiplicative inverse extends to matrices. The multiplicative inverse of a matrix ![]() (if it exists) is called the inverse matrix, denoted as
(if it exists) is called the inverse matrix, denoted as ![]() , such that:
, such that:
![]()
where ![]() is the identity matrix.
is the identity matrix.
- Illustrative Explanation: If you have a
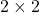 matrix
matrix  :
:
![]()
The inverse can be calculated (if ![]() ) as:
) as:
![]()
This property is crucial in solving systems of linear equations.
3.4. Computer Science
In computer science, the multiplicative inverse is used in algorithms, particularly in cryptography and numerical methods. It is essential for operations involving modular arithmetic.
- Illustrative Explanation: In modular arithmetic, finding the multiplicative inverse of a number
 modulo
modulo 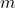 is crucial for operations such as division. The multiplicative inverse
is crucial for operations such as division. The multiplicative inverse 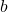 satisfies:
satisfies:
![]()
This is particularly important in algorithms like the Extended Euclidean Algorithm.
Conclusion
In conclusion, the multiplicative inverse is a fundamental mathematical concept that allows us to find the value that, when multiplied by a given number, yields the multiplicative identity ![]() . It has several important properties, including its existence for non-zero numbers, its relationship with fractions, and its application in algebraic structures. The multiplicative inverse is widely used in solving equations, working with fractions, matrix inversion, and various applications in computer science. By understanding the multiplicative inverse and its properties, we gain valuable insights into its relevance in mathematical analysis and real-world applications. As we continue to explore mathematics and its applications, the knowledge of the multiplicative inverse will remain a key component of our mathematical toolkit.
. It has several important properties, including its existence for non-zero numbers, its relationship with fractions, and its application in algebraic structures. The multiplicative inverse is widely used in solving equations, working with fractions, matrix inversion, and various applications in computer science. By understanding the multiplicative inverse and its properties, we gain valuable insights into its relevance in mathematical analysis and real-world applications. As we continue to explore mathematics and its applications, the knowledge of the multiplicative inverse will remain a key component of our mathematical toolkit.