Non-uniform motion is a fundamental concept in physics that describes the movement of an object when it travels at varying speeds or changes direction over time. Unlike uniform motion, where an object moves at a constant speed in a straight line, non-uniform motion involves acceleration or deceleration, making it a more complex and interesting topic. This article will provide a detailed exploration of non-uniform motion, including its definition, characteristics, types, equations of motion, applications, and significance, along with illustrative explanations to enhance understanding.
1. Definition of Non-Uniform Motion
Non-uniform motion refers to the motion of an object when its velocity changes over time. This change can occur in two ways: either the speed of the object varies, or the direction of motion changes, or both. In mathematical terms, non-uniform motion can be described as motion with a non-zero acceleration, meaning that the rate of change of velocity is not constant.
Illustrative Explanation: Imagine a car driving on a winding road. As the driver accelerates to overtake another vehicle, slows down to navigate a sharp turn, and then speeds up again on a straight stretch, the car is exhibiting non-uniform motion. The speed and direction of the car are constantly changing, illustrating the essence of non-uniform motion.
2. Characteristics of Non-Uniform Motion
A. Variable Speed
In non-uniform motion, the speed of the object is not constant. It can increase (acceleration) or decrease (deceleration) at different points in time.
Illustrative Explanation: Consider a runner in a race. At the start, the runner may sprint quickly (high speed), then slow down to conserve energy (low speed), and finally speed up again as they approach the finish line. This variation in speed exemplifies non-uniform motion.
B. Changing Direction
Non-uniform motion can also involve changes in direction, even if the speed remains constant. For example, an object moving in a circular path is constantly changing direction, which means it is undergoing non-uniform motion.
Illustrative Explanation: Picture a child swinging on a swing set. As the swing moves back and forth, the child is constantly changing direction, even if the speed of the swing remains relatively constant. This change in direction is a key characteristic of non-uniform motion.
C. Acceleration
Acceleration is a crucial aspect of non-uniform motion. It is defined as the rate of change of velocity over time. In non-uniform motion, the acceleration can be positive (speeding up), negative (slowing down), or even zero (constant speed).
Illustrative Explanation: Imagine a roller coaster. As the coaster climbs to the top of a hill, it slows down (negative acceleration). Once it reaches the peak and begins to descend, it speeds up (positive acceleration). The varying acceleration throughout the ride illustrates the concept of non-uniform motion.
3. Types of Non-Uniform Motion
A. Accelerated Motion
Accelerated motion occurs when an object’s speed increases over time. This can happen in a straight line or along a curved path. The acceleration can be uniform (constant) or non-uniform (varying).
Illustrative Explanation: Think of a car accelerating from a stoplight. As the light turns green, the driver presses the gas pedal, and the car speeds up. If the driver gradually increases the pressure on the pedal, the acceleration is uniform. If the driver suddenly floors the pedal, the acceleration is non-uniform.
B. Decelerated Motion
Decelerated motion is the opposite of accelerated motion, where an object’s speed decreases over time. Like accelerated motion, deceleration can also be uniform or non-uniform.
Illustrative Explanation: Imagine a bicycle rider approaching a stop sign. As the rider nears the sign, they apply the brakes, causing the bike to slow down. If the rider applies the brakes gently, the deceleration is uniform. If they brake suddenly, the deceleration is non-uniform.
C. Cyclic Motion
Cyclic motion refers to motion that repeats itself in a regular cycle, such as the motion of a pendulum or a wheel. While the speed may vary at different points in the cycle, the overall motion is periodic.
Illustrative Explanation: Picture a pendulum swinging back and forth. At the highest points of its swing, the pendulum moves slowly (low speed), while at the lowest point, it moves quickly (high speed). This variation in speed during a repeating cycle exemplifies cyclic non-uniform motion.
4. Equations of Motion for Non-Uniform Motion
In non-uniform motion, the equations of motion can be more complex than those for uniform motion. The following equations are commonly used to describe non-uniform motion, particularly in the context of linear motion with constant acceleration:
1. First Equation of Motion:
![\[ v = u + at \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a4bbe9a22197edd7a53649794e57731a_l3.png "Rendered by QuickLaTeX.com")
Where:
= final velocity
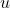= initial velocity
= acceleration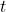
= time
2. Second Equation of Motion:
![\[ s = ut + \frac{1}{2}at^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-956d5e2bc9705ff9ab425504deee779c_l3.png "Rendered by QuickLaTeX.com")
Where:
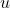= displacement- = initial velocity
- = acceleration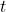
- = time
3. Third Equation of Motion:
![\[ v^2 = u^2 + 2as \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-1bc3e62b915210541fb0882da789d0c3_l3.png "Rendered by QuickLaTeX.com")
Where:
- = final velocity
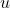- = initial velocity
- = acceleration
- = displacement
Illustrative Explanation: Consider a car that starts from rest (initial velocity 
) and accelerates at a constant rate of 
for 
seconds. Using the first equation of motion, we can calculate the final velocity () as follows:
![\[ v = 0 + (2 \, \text{m/s}^2)(5 \, \text{s}) = 10 \, \text{m/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-83acd15822e3839e1448041ae92c9a8c_l3.png "Rendered by QuickLaTeX.com")
This calculation illustrates how the equations of motion can be applied to analyze non-uniform motion.
5. Applications of Non-Uniform Motion
A. Transportation
Understanding non-uniform motion is crucial in the design and operation of vehicles, airplanes, and other modes of transportation. Engineers must account for varying speeds and accelerations to ensure safety and efficiency.
Illustrative Explanation: Think of a train traveling on a track. As it approaches a station, it must decelerate smoothly to come to a stop. Engineers design the braking system to manage this non-uniform motion effectively, ensuring a safe arrival.
B. Sports Science
In sports, athletes often exhibit non-uniform motion during their performances. Coaches and trainers analyze these movements to improve techniques, enhance performance, and reduce the risk of injury.
Illustrative Explanation: Imagine a sprinter running a race. The sprinter accelerates at the start, maintains a high speed in the middle, and then decelerates as they approach the finish line. Coaches study this non-uniform motion to help athletes optimize their performance.
C. Robotics and Automation
In robotics, understanding non-uniform motion is essential for programming robots to perform tasks efficiently. Robots must navigate varying speeds and directions to complete their functions accurately.
Illustrative Explanation: Picture a robotic arm assembling parts on a production line. The arm must move quickly to pick up a part, slow down to position it accurately, and then speed up again to move to the next task. This non-uniform motion is critical for the robot’s efficiency.
6. Significance of Non-Uniform Motion
A. Real-World Relevance
Non-uniform motion is a common occurrence in everyday life. From driving a car to playing sports, understanding how objects move in non-uniform ways helps us navigate the world around us.
Illustrative Explanation: Think of a busy city street. Cars, bicycles, and pedestrians all exhibit non-uniform motion as they accelerate, decelerate, and change direction. Recognizing these patterns helps us understand traffic flow and safety.
B. Scientific Understanding
Studying non-uniform motion contributes to our understanding of fundamental physics concepts, such as force, energy, and momentum. It allows scientists to analyze and predict the behavior of objects in motion.
Illustrative Explanation: Imagine a scientist conducting an experiment with a rolling ball. By measuring the ball’s speed and direction at various points, the scientist gains insights into the forces acting on the ball, enhancing our understanding of motion.
C. Technological Advancements
Advancements in technology often rely on principles of non-uniform motion. Engineers and designers use these principles to create innovative solutions in transportation, robotics, and other fields.
Illustrative Explanation: Consider the development of self-driving cars. Engineers must program the vehicles to navigate non-uniform motion safely, adjusting speeds and directions in real-time to respond to changing road conditions.
7. Conclusion
In summary, non-uniform motion is a fundamental concept in physics that describes the movement of objects when their speed or direction changes over time. It encompasses various characteristics, types, and equations of motion, making it a complex yet fascinating topic. Understanding non-uniform motion is essential for applications in transportation, sports science, robotics, and many other fields. Whether you are a student, a researcher, or simply curious about the world around you, a solid understanding of non-uniform motion will deepen your appreciation for the intricate processes that govern the behavior of objects in motion. Non-uniform motion is not just a theoretical concept; it is a key aspect of our daily lives, influencing everything from how we travel to how we interact with the world around us