Ohm’s Law is a fundamental principle in electrical engineering and physics that describes the relationship between voltage, current, and resistance in an electrical circuit. Formulated by the German physicist Georg Simon Ohm in the 1820s, this law provides a foundational understanding of how electrical circuits operate. Ohm’s Law is essential for analyzing and designing electrical systems, making it a cornerstone of both theoretical and practical applications in electronics. This article aims to provide a comprehensive understanding of Ohm’s Law, including its formulation, derivation, applications, limitations, and significance in modern technology.
Historical Background
Georg Simon Ohm published his groundbreaking work, “Die galvanische Kette, mathematisch bearbeitet” (The Galvanic Circuit Investigated Mathematically), in 1827. In this work, he introduced the concept of resistance and established the relationship between voltage, current, and resistance, which would later be known as Ohm’s Law. Ohm’s experiments involved measuring the current flowing through various conductors while varying the voltage applied across them. His findings demonstrated that the current flowing through a conductor is directly proportional to the voltage across it and inversely proportional to the resistance of the conductor.
Ohm’s Law was initially met with skepticism, but it eventually gained acceptance and became a fundamental principle in electrical engineering. The law has since been instrumental in the development of electrical theory and the design of circuits, influencing countless innovations in technology.
Formulation of Ohm’s Law
Ohm’s Law can be mathematically expressed as:
![\[ V = I \cdot R \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-014371ce2fbe9ad858c423ce9bed1998_l3.png "Rendered by QuickLaTeX.com")
Where:
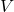is the voltage (potential difference) across the conductor, measured in volts (V).
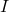is the current flowing through the conductor, measured in amperes (A).
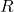is the resistance of the conductor, measured in ohms (Ω).
This equation indicates that the voltage across a conductor is equal to the product of the current flowing through it and the resistance of the conductor. The relationship can also be rearranged to solve for current or resistance:
1. To find current:
![\[ I = \frac{V}{R} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-ad1bfc02188b19cc7f78453fc02955e2_l3.png "Rendered by QuickLaTeX.com")
2. To find resistance:
![\[ R = \frac{V}{I} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-e4d211b38b2147bbe328c3fab371cc87_l3.png "Rendered by QuickLaTeX.com")
Understanding the Components of Ohm’s Law
1. Voltage (V): Voltage, or electric potential difference, is the force that pushes electric charges through a circuit. It is analogous to the pressure in a water system that drives water through pipes. Voltage is measured in volts (V), and it represents the energy per unit charge available to move electrons through a conductor.
2. Current (I): Current is the flow of electric charge in a circuit, measured in amperes (A). It represents the rate at which charge flows through a conductor. Current can be thought of as the flow of water in a pipe, where a higher current indicates a greater flow of charge.
3. Resistance (R): Resistance is the opposition to the flow of electric current in a conductor, measured in ohms (Ω). It depends on the material, length, and cross-sectional area of the conductor. Materials with low resistance, such as copper and aluminum, are good conductors, while materials with high resistance, such as rubber and glass, are insulators.
Derivation of Ohm’s Law
The derivation of Ohm’s Law is based on experimental observations and the behavior of electric circuits. The relationship can be understood through the following concepts:
1. Proportionality: Ohm observed that for a given conductor, the current flowing through it is directly proportional to the voltage applied across it. This means that if the voltage increases, the current also increases, provided the resistance remains constant.
2. Constant Resistance: Ohm’s Law holds true for many materials under constant temperature and physical conditions. The resistance of a conductor remains relatively constant for small changes in voltage and current, allowing for a linear relationship between the two.
3. Linear Relationship: The relationship between voltage and current can be graphically represented as a straight line on a voltage-current (V-I) graph. The slope of this line represents the resistance of the conductor. For ohmic materials, this linearity is maintained, confirming the validity of Ohm’s Law.
Applications of Ohm’s Law
Ohm’s Law has numerous applications across various fields, including:
1. Circuit Analysis: Ohm’s Law is fundamental in analyzing electrical circuits. Engineers and technicians use it to calculate the current, voltage, and resistance in series and parallel circuits, enabling them to design and troubleshoot electrical systems effectively.
2. Power Calculations: Ohm’s Law is used in conjunction with the power formula to calculate electrical power consumption in circuits. The power (
) consumed by a resistor can be expressed as:
![\[ P = V \cdot I = I^2 \cdot R = \frac{V^2}{R} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-998ee8abd5dc32435c6d00ab9d4748fc_l3.png "Rendered by QuickLaTeX.com")
This relationship allows for the determination of power loss in resistive components, which is crucial for efficient circuit design.
3. Component Selection: When designing circuits, engineers use Ohm’s Law to select appropriate components, such as resistors, capacitors, and inductors, ensuring that the circuit operates within desired parameters.
4. Safety and Protection: Ohm’s Law is essential for determining safe operating conditions for electrical devices. By calculating the current flowing through a circuit, engineers can ensure that components are not overloaded, preventing overheating and potential failure.
5. Instrumentation: Ohm’s Law is used in various measuring instruments, such as multimeters and oscilloscopes, to measure voltage, current, and resistance accurately.
Limitations of Ohm’s Law
While Ohm’s Law is a powerful tool, it has certain limitations:
1. Non-Ohmic Materials: Ohm’s Law applies primarily to ohmic materials, which exhibit a linear relationship between voltage and current. Non-ohmic materials, such as diodes and transistors, do not follow Ohm’s Law, as their resistance varies with voltage and current.
2. Temperature Dependence: The resistance of most materials changes with temperature. For significant temperature variations, the linear relationship described by Ohm’s Law may not hold true, necessitating adjustments to account for temperature effects.
3. High Frequencies: At high frequencies, the behavior of electrical components can become complex due to factors such as inductance and capacitance. In such cases, the simple application of Ohm’s Law may not accurately describe circuit behavior.
4. Complex Circuits: In circuits with multiple components and configurations, the application of Ohm’s Law may require more advanced techniques, such as Kirchhoff’s laws or network analysis, to fully understand the interactions between components.
Conclusion
Ohm’s Law is a fundamental principle that underpins the study and application of electrical circuits. Its formulation, derivation, and wide-ranging applications make it an essential tool for engineers, technicians, and students in the field of electrical engineering and physics. Despite its limitations, Ohm’s Law remains a cornerstone of electrical theory, providing valuable insights into the behavior of electrical systems. Understanding Ohm’s Law not only enhances our knowledge of electricity but also equips us with the tools necessary to design, analyze, and troubleshoot electrical circuits effectively. As technology continues to evolve, the principles encapsulated in Ohm’s Law will remain integral to the development of innovative solutions in electronics, energy systems, and beyond.