Pentagonal Prism: A Comprehensive Exploration

A pentagonal prism is a three-dimensional geometric shape that is classified as a type of prism. It is characterized by its two parallel pentagonal bases and five rectangular lateral faces. Understanding the properties, characteristics, and applications of pentagonal prisms is essential in fields such as geometry, architecture, engineering, and various scientific disciplines. This article will delve into the definition of a pentagonal prism, its properties, formulas for calculating its volume and surface area, and its applications, providing illustrative explanations for each concept.

Definition of a Pentagonal Prism

A pentagonal prism is defined as a polyhedron with two parallel bases that are pentagons and five rectangular faces connecting the corresponding sides of the two bases. The bases are congruent, meaning they have the same shape and size, and the lateral faces are perpendicular to the bases.

Visual Representation

To visualize a pentagonal prism, imagine a box-like structure where the top and bottom faces are pentagons. If you were to look at the prism from the side, you would see five rectangles connecting the two pentagonal bases. This structure can be likened to a stack of books where each book has a pentagonal cover.

Properties of a Pentagonal Prism

1. Faces, Edges, and Vertices:
– A pentagonal prism has a total of 7 faces: 2 pentagonal bases and 5 rectangular lateral faces.
– It has 15 edges: 5 edges on each pentagonal base (10 edges total) and 5 edges connecting the corresponding vertices of the two bases.
– It has 10 vertices: 5 vertices on the top pentagonal base and 5 vertices on the bottom pentagonal base.

2. Congruent Bases:
– The two pentagonal bases are congruent, meaning they are identical in shape and size. This property is crucial for maintaining the uniformity of the prism.

3. Lateral Faces:
– The lateral faces of a pentagonal prism are rectangles. Each rectangle connects one side of the top pentagon to the corresponding side of the bottom pentagon.

Formulas for Volume and Surface Area

Understanding how to calculate the volume and surface area of a pentagonal prism is essential for practical applications in various fields.

Volume of a Pentagonal Prism

The volume $V$ of a pentagonal prism can be calculated using the formula:

$V = B \times h$

where:

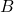$B$ is the area of the pentagonal base.
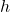$h$ is the height of the prism (the perpendicular distance between the two bases).

To find the area $B$ of a regular pentagon, you can use the formula:

$B = \frac{1}{4} \sqrt{5(5 + 2\sqrt{5})} s^2$

where $s$ is the length of a side of the pentagon.

Example:
If the side length of the pentagonal base is $s = 4$ units and the height of the prism is $h = 10$ units, the area of the base is:

$B = \frac{1}{4} \sqrt{5(5 + 2\sqrt{5})} (4^2) \approx 27.527 \text{ square units}$

Thus, the volume of the prism is:

$V = 27.527 \times 10 \approx 275.27 \text{ cubic units}$

Surface Area of a Pentagonal Prism

The surface area $A$ of a pentagonal prism can be calculated using the formula:

$A = 2B + L$

where:

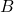$B$ is the area of the pentagonal base.
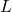$L$ is the lateral surface area, which can be calculated as:

$L = \text{Perimeter of the base} \times h$

The perimeter $P$ of a regular pentagon is given by:

$P = 5s$

Example:
Continuing with the previous example, if $s = 4$ units, the perimeter of the base is:

$P = 5 \times 4 = 20 \text{ units}$

The lateral surface area is:

$L = 20 \times 10 = 200 \text{ square units}$

Now, substituting back into the surface area formula:

$A = 2B + L = 2(27.527) + 200 \approx 55.054 + 200 = 255.054 \text{ square units}$

Applications of Pentagonal Prisms

Pentagonal prisms have various applications across different fields:

1. Architecture: The unique shape of pentagonal prisms can be utilized in architectural designs, creating visually appealing structures. They can be used in the design of buildings, pavilions, and other architectural elements.

2. Engineering: In engineering, pentagonal prisms can be used in the design of components that require a specific structural integrity and aesthetic appeal. They can be found in various mechanical parts and systems.

3. Mathematics and Geometry: Pentagonal prisms are studied in geometry to understand the properties of three-dimensional shapes. They serve as examples in teaching concepts related to volume, surface area, and spatial reasoning.

4. Art and Design: Artists and designers may use pentagonal prisms in their work to create sculptures, installations, and other artistic expressions. The geometric nature of the prism can inspire creativity and innovation.

5. Packaging: The pentagonal prism shape can be used in packaging design, particularly for products that benefit from a unique and recognizable shape. This can enhance branding and consumer appeal.

Conclusion

In conclusion, the pentagonal prism is a fascinating geometric shape characterized by its two parallel pentagonal bases and five rectangular lateral faces. Understanding its properties, formulas for volume and surface area, and applications in various fields provides valuable insights into the world of geometry and its practical implications. Whether in architecture, engineering, or art, the pentagonal prism serves as a versatile and significant shape that continues to inspire creativity and innovation. By mastering the concepts related to pentagonal prisms, individuals can enhance their mathematical skills and appreciation for the beauty of geometric forms in the world around them.

Blog.Pengayaan.Com