Perfect Cubes of Numbers: A Comprehensive Overview

In mathematics, the concept of perfect cubes is an essential topic that arises in various fields, including algebra, number theory, and geometry. A perfect cube is a number that can be expressed as the cube of an integer. Understanding perfect cubes is crucial for solving problems related to volume, polynomial equations, and even in real-world applications such as architecture and engineering. This article will explore the definition of perfect cubes, their properties, methods for identifying them, and illustrative examples to enhance comprehension.

What is a Perfect Cube?

Definition of a Perfect Cube

A perfect cube is a number that can be expressed in the form $n^3$ , where $n$ is an integer. In other words, when an integer is multiplied by itself twice (i.e., multiplied three times), the result is a perfect cube.

Illustrative Explanation: Imagine you have a cube-shaped box. If the length of each side of the box is an integer, the volume of the box (which is calculated as side length cubed) will be a perfect cube. For example, if each side of the box is 3 units long, the volume is 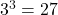$3^3 = 27$ cubic units, which is a perfect cube.

Examples of Perfect Cubes

Here are some examples of perfect cubes:

$1^3 = 1$
$2^3 = 8$
$3^3 = 27$
$4^3 = 64$
$5^3 = 125$
$6^3 = 216$
$7^3 = 343$
$8^3 = 512$
$9^3 = 729$
$10^3 = 1000$

These numbers (1, 8, 27, 64, 125, 216, 343, 512, 729, and 1000) are all perfect cubes because they can be expressed as the cube of an integer.

Properties of Perfect Cubes

Understanding the properties of perfect cubes is essential for recognizing and working with them effectively. Here are some key properties:

1. Integer Roots

The cube root of a perfect cube is always an integer. For example, the cube root of 64 is 4, since $4^3 = 64$ .

Illustrative Explanation: If you have a perfect cube, such as 125, you can find its cube root by determining which integer, when multiplied by itself three times, gives you 125. In this case, 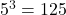$5^3 = 125$ , so the cube root of 125 is 5.

2. Odd and Even Perfect Cubes

Perfect cubes can be either odd or even, depending on the integer being cubed. If the integer is odd, the perfect cube will also be odd; if the integer is even, the perfect cube will be even.

Illustrative Explanation: Consider the perfect cubes of 2 and 3. The cube of 2 (an even integer) is 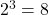$2^3 = 8$ (even), while the cube of 3 (an odd integer) is 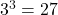$3^3 = 27$ (odd). This property holds true for all integers.

3. Sum of Perfect Cubes

The sum of two or more perfect cubes can yield another perfect cube, but this is not always the case. For example, $1^3 + 2^3 = 1 + 8 = 9$ , which is not a perfect cube. However, $1^3 + 3^3 = 1 + 27 = 28$ , which is also not a perfect cube.

Illustrative Explanation: If you take the perfect cubes of 1 and 2, you get 1 and 8, respectively. Adding them gives you 9, which is not a perfect cube. However, if you take 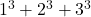$1^3 + 2^3 + 3^3$ , you get 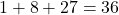$1 + 8 + 27 = 36$ , which is also not a perfect cube. This illustrates that while some combinations may yield perfect cubes, it is not a guaranteed outcome.

4. Difference of Perfect Cubes

The difference between two perfect cubes can be factored using the formula:

$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$

This property is useful in algebraic manipulations and solving equations.

Illustrative Explanation: If you take 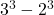$3^3 - 2^3$ , you have 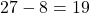$27 - 8 = 19$ . Using the formula, you can factor it as follows:

– $a = 3$ and $b = 2$
– $3^3 - 2^3 = (3 - 2)(3^2 + 3 \cdot 2 + 2^2)$
– $= 1(9 + 6 + 4) = 1 \cdot 19 = 19$

Identifying Perfect Cubes

Method 1: Direct Calculation

The simplest way to identify perfect cubes is to calculate the cubes of integers. For example, you can calculate $1^3$ , $2^3$ , $3^3$ , and so on, until you reach the desired range.

Method 2: Cube Root Calculation

You can also determine if a number is a perfect cube by calculating its cube root. If the cube root is an integer, then the number is a perfect cube.

Illustrative Explanation: To check if 64 is a perfect cube, calculate the cube root:

– $\sqrt[3]{64} = 4$
– Since 4 is an integer, 64 is a perfect cube.

Method 3: Prime Factorization

Another method to identify perfect cubes is through prime factorization. A number is a perfect cube if all the prime factors have exponents that are multiples of 3.

Illustrative Explanation: Consider the number 216. Its prime factorization is:

– $216 = 2^3 \times 3^3$
– Both exponents (3 and 3) are multiples of 3, indicating that 216 is a perfect cube ( $6^3$ ).

Applications of Perfect Cubes

Perfect cubes have various applications in mathematics and real-world scenarios:

1. Geometry

In geometry, perfect cubes are used to calculate the volume of cube-shaped objects. The volume $V$ of a cube is given by the formula:

$V = s^3$

where $s$ is the length of a side of the cube.

Illustrative Explanation: If a cube has a side length of 4 units, its volume is 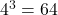$4^3 = 64$ cubic units.

2. Algebra

Perfect cubes are often encountered in algebraic expressions and equations. They can be factored or expanded using the properties of cubes, which is useful in solving polynomial equations.

3. Number Theory

In number theory, perfect cubes are studied for their properties and relationships with other numbers. They play a role in various theorems and conjectures related to integers.

4. Real-World Applications

Perfect cubes can be found in various real-world applications, such as calculating the volume of storage containers, determining the amount of material needed for construction, and in computer graphics for rendering 3D objects.

Conclusion

Perfect cubes are a fundamental concept in mathematics, representing numbers that can be expressed as the cube of an integer. Understanding perfect cubes, their properties, and methods for identifying them is essential for solving mathematical problems and applying these concepts in various fields. From geometry to algebra and number theory, perfect cubes play a significant role in our understanding of numbers and their relationships. As we continue to explore the world of mathematics, the concept of perfect cubes will remain an important tool in our mathematical toolkit, enabling us to analyze and interpret numerical relationships effectively.

Blog.Pengayaan.Com