Perfect Numbers: A Comprehensive Exploration

Perfect numbers are a fascinating concept in number theory, representing a unique class of integers that have intrigued mathematicians for centuries. A perfect number is defined as a positive integer that is equal to the sum of its proper divisors, excluding itself. This article aims to provide an exhaustive overview of perfect numbers, detailing their definitions, properties, historical significance, examples, and illustrative explanations for each concept.

1. Definition of Perfect Numbers

1.1. What are Perfect Numbers?

A perfect number is a positive integer $n$ such that the sum of its proper divisors (the divisors of $n$ excluding $n$ itself) is equal to $n$ . Mathematically, this can be expressed as:

$\sigma(n) - n = n$

where $\sigma(n)$ is the sum of all divisors of $n$ . This can be simplified to:

$\sigma(n) = 2n$

1.2. Examples of Perfect Numbers

The smallest perfect numbers are:

1. 6: The divisors of $6$ are $1, 2, 3, 6$ . The sum of the proper divisors is $1 + 2 + 3 = 6$ .
2. 28: The divisors of $28$ are $1, 2, 4, 7, 14, 28$ . The sum of the proper divisors is $1 + 2 + 4 + 7 + 14 = 28$ .
3. 496: The divisors of $496$ are $1, 2, 4, 8, 16, 31, 62, 124, 248, 496$ . The sum of the proper divisors is $1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496$ .
4. 8128: The divisors of $8128$ are $1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064, 8128$ . The sum of the proper divisors is $1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064 = 8128$ .

Illustrative Explanation: To understand perfect numbers, consider the number $6$ . Its proper divisors are $1, 2, 3$ . When you add these divisors together, you get $6$ , which is exactly the number itself, thus making $6$ a perfect number.

2. Properties of Perfect Numbers

2.1. Even Perfect Numbers

All known perfect numbers are even, and they can be expressed in the form:

$P = 2^{p-1}(2^p - 1)$

where both $p$ and $2^p - 1$ are prime numbers. The term $2^p - 1$ is known as a Mersenne prime.

Illustrative Explanation: For example, if $p = 3$ , then $2^3 - 1 = 7$ (which is prime). Thus, the perfect number is:

$P = 2^{3-1}(2^3 - 1) = 2^2 \times 7 = 28$

2.2. Odd Perfect Numbers

As of now, no odd perfect numbers have been discovered, and it remains an open question in mathematics whether any exist. If they do exist, they must satisfy certain conditions, such as being greater than $10^{1500}$ and having at least $101$ prime factors.

2.3. Relationship with Mersenne Primes

Perfect numbers are closely related to Mersenne primes. A Mersenne prime is a prime number of the form $2^p - 1$ . If $2^p - 1$ is prime, then $2^{p-1}(2^p - 1)$ is a perfect number.

Illustrative Explanation: For instance, if $p = 5$ , then $2^5 - 1 = 31$ (which is prime). The corresponding perfect number is:

$P = 2^{5-1}(2^5 - 1) = 2^4 \times 31 = 496$

3. Historical Significance of Perfect Numbers

3.1. Ancient Civilizations

The study of perfect numbers dates back to ancient civilizations. The Greek mathematician Euclid (circa 300 BC) was one of the first to study perfect numbers. He established the relationship between even perfect numbers and Mersenne primes.

3.2. Medieval Mathematics

In the Middle Ages, mathematicians continued to explore perfect numbers. The Persian mathematician Al-Khwarizmi and the Italian mathematician Leonardo of Pisa (Fibonacci) contributed to the understanding of these numbers.

3.3. Modern Mathematics

In modern mathematics, perfect numbers have been studied extensively in number theory. The search for Mersenne primes and perfect numbers continues to be an area of active research, with advancements in computational techniques allowing mathematicians to discover larger perfect numbers.

4. Examples of Perfect Numbers in Detail

Example 1: The Perfect Number 6

Divisors: $1, 2, 3, 6$
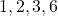
Sum of Proper Divisors: $1 + 2 + 3 = 6$
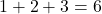
Conclusion: Since the sum of the proper divisors equals the number itself, 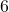$6$ is a perfect number.

Example 2: The Perfect Number 28

Divisors: $1, 2, 4, 7, 14, 28$
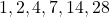
Sum of Proper Divisors: $1 + 2 + 4 + 7 + 14 = 28$
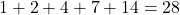
Conclusion: The sum of the proper divisors equals 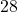$28$ , confirming it as a perfect number.

Example 3: The Perfect Number 496

Divisors: $1, 2, 4, 8, 16, 31, 62, 124, 248, 496$
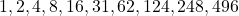
Sum of Proper Divisors: $1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496$
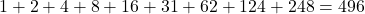
Conclusion: The sum of the proper divisors equals 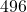$496$ , making it a perfect number.

Example 4: The Perfect Number 8128

Divisors: $1, 2, 4, 8, 16, 32, 127, 254, 508, 1016, 2032, 4064, 8128$
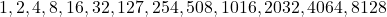
Sum of Proper Divisors: $1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064 = 8128$
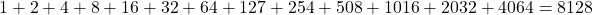
Conclusion: The sum of the proper divisors equals 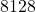$8128$ , confirming it as a perfect number.

5. Applications of Perfect Numbers

5.1. Mathematical Research

Perfect numbers are studied in number theory and have implications in various mathematical fields, including algebra and combinatorics. They help mathematicians understand the properties of integers and their relationships.

5.2. Cryptography

While not directly used in cryptography, the study of perfect numbers and their properties can contribute to the understanding of prime numbers, which are fundamental in cryptographic algorithms.

5.3. Computer Science

Perfect numbers and their relationships with Mersenne primes can be explored in computer algorithms, particularly in the context of prime number generation and testing.

6. Limitations and Open Questions

6.1. Existence of Odd Perfect Numbers

The existence of odd perfect numbers remains one of the most significant unsolved problems in mathematics. Despite extensive research, no odd perfect numbers have been found, and it is unclear whether they exist.

6.2. Computational Challenges

Finding larger perfect numbers requires significant computational resources. As the numbers grow, the search for Mersenne primes becomes increasingly complex, necessitating advanced algorithms and powerful computers.

Conclusion

In conclusion, perfect numbers are a captivating concept in number theory, defined as positive integers equal to the sum of their proper divisors. The exploration of perfect numbers has a rich historical background, with contributions from ancient civilizations to modern mathematics. While all known perfect numbers are even and closely related to Mersenne primes, the existence of odd perfect numbers remains an open question. Understanding perfect numbers is essential for mathematicians and enthusiasts alike, as they provide insight into the properties of integers and the relationships between numbers. As we continue to explore the vast landscape of mathematics, the study of perfect numbers will remain a vital area of research, inspiring curiosity and discovery in the world of numbers.

Blog.Pengayaan.Com