Periodic motion is a type of motion that repeats itself at regular intervals of time. This concept is fundamental in various fields of physics and engineering, as it describes the behavior of systems that oscillate or cycle through a series of positions. Examples of periodic motion can be found in everyday life, from the swinging of a pendulum to the vibrations of a guitar string. Understanding periodic motion involves exploring its definition, characteristics, types, mathematical descriptions, and applications. This article aims to provide an exhaustive overview of periodic motion, detailing each aspect with illustrative explanations.
Understanding Periodic Motion
1. Definition of Periodic Motion
Periodic motion refers to any motion that occurs in a regular, repeating pattern over time. In such motion, an object returns to its initial position after a fixed duration, known as the period. The period is the time taken to complete one full cycle of motion.
- Illustrative Explanation: Imagine a Ferris wheel at an amusement park. As the wheel rotates, each passenger experiences a complete ride, returning to their starting point after a specific amount of time. This repetitive cycle exemplifies periodic motion, where the time taken for one complete rotation is the period.
2. Characteristics of Periodic Motion
Periodic motion exhibits several key characteristics that define its behavior:
a. Period (T)
The period is the time taken to complete one full cycle of motion. It is typically measured in seconds (s). The period is a crucial parameter in understanding the frequency and behavior of periodic systems.
- Illustrative Explanation: Consider a clock’s second hand. It takes 60 seconds to complete one full rotation. This duration is the period of the second hand’s motion.
b. Frequency (f)
Frequency is the number of complete cycles that occur in one second. It is the reciprocal of the period and is measured in hertz (Hz). The relationship between frequency and period is given by the formula:
![\[ f = \frac{1}{T} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b73d511df851ecb42dcf05d41e548c51_l3.png "Rendered by QuickLaTeX.com")
Where:
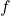is the frequency,
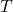is the period.- Illustrative Explanation: Imagine a child on a swing. If the swing completes 10 full back-and-forth motions in one minute, the frequency of the swing’s motion is
.
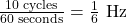c. Amplitude (A)
Amplitude is the maximum displacement of an object from its equilibrium position during periodic motion. It represents the extent of the motion and is a measure of how far the object moves from its central position.
- Illustrative Explanation: Picture a pendulum swinging back and forth. The highest point it reaches on either side of its central position is the amplitude. If the pendulum swings 30 degrees to the left and 30 degrees to the right, the amplitude is the maximum angle of 30 degrees.
d. Phase
The phase of periodic motion describes the position of the object in its cycle at a specific point in time. It is often expressed in degrees or radians and helps determine the state of motion at any given moment.
- Illustrative Explanation: Imagine a circular track where runners start at different points. If one runner is at the starting line (0 degrees), another might be halfway around the track (180 degrees). The phase indicates where each runner is in their respective cycles.
3. Types of Periodic Motion
Periodic motion can be classified into several types based on the nature of the motion and the forces involved:
a. Simple Harmonic Motion (SHM)
Simple harmonic motion is a specific type of periodic motion characterized by a restoring force that is directly proportional to the displacement from the equilibrium position. SHM is often described by sinusoidal functions and is exemplified by systems like springs and pendulums.
- Illustrative Explanation: Consider a mass attached to a spring. When the mass is pulled and released, it oscillates back and forth around its equilibrium position. The motion is periodic, and the restoring force of the spring pulls the mass back toward the center, creating a smooth, repetitive motion.
b. Damped Motion
Damped motion occurs when periodic motion gradually decreases in amplitude over time due to the presence of resistive forces, such as friction or air resistance. The energy of the system is dissipated, leading to a reduction in the motion’s intensity.
- Illustrative Explanation: Imagine a swing that gradually slows down after being pushed. The air resistance and friction at the pivot point cause the swing to lose energy, resulting in a decrease in the amplitude of its motion until it eventually comes to a stop.
c. Forced Motion
Forced motion occurs when an external periodic force is applied to a system, causing it to oscillate at a frequency determined by the external force rather than its natural frequency. This can lead to resonance if the frequency of the external force matches the system’s natural frequency.
- Illustrative Explanation: Picture a child on a swing being pushed by a friend. If the friend pushes at just the right moments (matching the swing’s natural frequency), the swing will go higher and higher, demonstrating resonance.
4. Mathematical Description of Periodic Motion
The mathematical description of periodic motion often involves sinusoidal functions, which can represent the position, velocity, and acceleration of an oscillating object. The general form of a sinusoidal function is:
![\[ x(t) = A \cos(\omega t + \phi) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d2cb301190a2f9252521f1013bf4ef14_l3.png "Rendered by QuickLaTeX.com")
Where:
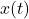is the displacement at time 
,
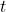is the amplitude,
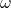is the angular frequency (related to the period),
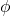is the phase constant.
a. Angular Frequency ()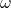
Angular frequency is related to the frequency and period of the motion. It is defined as:
![\[ \omega = 2\pi f = \frac{2\pi}{T} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8307375ab9cc92df0a3b4825b17d7e2e_l3.png "Rendered by QuickLaTeX.com")
Where:
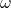- is the angular frequency (in radians per second),
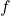- is the frequency (in hertz),
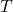- is the period (in seconds).
- Illustrative Explanation: Imagine a Ferris wheel rotating. The angular frequency represents how quickly the wheel turns in radians per second. If the wheel completes one full rotation (2π radians) in 60 seconds, the angular frequency is
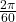radians per second.
5. Applications of Periodic Motion
Periodic motion has numerous applications across various fields, including:
a. Engineering and Design
Understanding periodic motion is crucial in engineering and design, particularly in the development of mechanical systems, such as clocks, engines, and suspension systems. Engineers must account for periodic motion to ensure the reliability and efficiency of these systems.
- Illustrative Explanation: Think of a car’s suspension system. The springs and shock absorbers are designed to handle the periodic motion of the car as it travels over bumps, ensuring a smooth ride.
b. Music and Acoustics
Periodic motion is fundamental in music and acoustics, as sound waves are periodic in nature. Instruments produce sound through vibrations, which create periodic waves that travel through the air.
- Illustrative Explanation: Imagine a guitar string being plucked. The string vibrates back and forth, creating sound waves that travel through the air. The frequency of the vibration determines the pitch of the sound produced.
c. Seismology
Periodic motion is essential in seismology, the study of earthquakes and seismic waves. Understanding the periodic nature of seismic waves helps scientists analyze and predict earthquake behavior.
- Illustrative Explanation: Picture a wave pool at a water park. When a large wave (seismic wave) travels through the water, it creates periodic ripples. Seismologists study these ripples to understand the energy released during an earthquake.
d. Biological Rhythms
Periodic motion is also observed in biological systems, such as circadian rhythms, which are the natural cycles that regulate various physiological processes in living organisms. These rhythms are essential for maintaining health and well-being.
- Illustrative Explanation: Think of a plant that opens its flowers during the day and closes them at night. This periodic behavior is driven by its internal biological clock, which regulates its activities based on the time of day.
Conclusion
In conclusion, periodic motion is a fundamental concept in physics that describes the repetitive behavior of systems over time. By exploring its definition, characteristics, types, mathematical descriptions, and applications, we can appreciate the significance of periodic motion in various fields of science and engineering. The study of periodic motion not only deepens our understanding of oscillatory systems but also highlights the importance of these principles in shaping the technologies and phenomena we encounter in our daily lives. As research in periodic motion continues to evolve, its applications will undoubtedly expand, paving the way for innovations that can benefit society as a whole. Understanding periodic motion is essential for anyone interested in physics, engineering, and the natural sciences, providing a foundation for further exploration of the fascinating world of oscillations and waves.