Prime factorization is a fundamental concept in number theory that involves expressing a number as the product of its prime factors. This technique is particularly useful when calculating the Highest Common Factor (HCF) and the Lowest Common Multiple (LCM) of two or more numbers. Understanding the prime factorization of HCF and LCM is essential for various applications in mathematics, including simplifying fractions, solving problems involving ratios, and working with divisibility. This article will delve into the definitions of HCF and LCM, the process of prime factorization, and how to find the HCF and LCM using prime factorization, along with illustrative explanations for each concept.
Definitions
Highest Common Factor (HCF)
The Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), is the largest positive integer that divides two or more numbers without leaving a remainder. The HCF is useful for simplifying fractions and finding common denominators.
Lowest Common Multiple (LCM)
The Lowest Common Multiple (LCM) is the smallest positive integer that is a multiple of two or more numbers. The LCM is essential for adding and subtracting fractions with different denominators and for solving problems involving multiples.
Prime Factorization
Prime factorization is the process of breaking down a composite number into its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. For example, the prime factorization of 12 is 
because 
.
Illustrative Explanation
To visualize prime factorization, consider the number 30. If you think of 30 as a group of objects, you can break it down into smaller groups of prime objects:
1. Start with 30 and divide it by the smallest prime number, which is 2. Since 30 is even, you can divide it:
![\[ 30 \div 2 = 15 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0fb5568cd4674b4acb09c08f6192ea38_l3.png "Rendered by QuickLaTeX.com")
So, one factor is 2.
2. Next, take 15 and divide it by the next smallest prime number, which is 3:
![\[ 15 \div 3 = 5 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-de68ca9182d659b15a45ca9a04bd2fdc_l3.png "Rendered by QuickLaTeX.com")
So, another factor is 3.
3. Finally, 5 is a prime number itself, so you stop here.
Thus, the prime factorization of 30 is:
![\[ 30 = 2^1 \times 3^1 \times 5^1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-6c51ddf3036007dfcc1aa3ea43696121_l3.png "Rendered by QuickLaTeX.com")
Finding HCF Using Prime Factorization
To find the HCF of two or more numbers using prime factorization, follow these steps:
1. Find the Prime Factorization: Determine the prime factorization of each number.
2. Identify Common Factors: Identify the common prime factors among the numbers.
3. Choose the Lowest Powers: For each common prime factor, choose the lowest power that appears in the factorizations.
4. Multiply the Common Factors: Multiply these common factors together to get the HCF.
Illustrative Example
Let’s find the HCF of 24 and 36.
1. Prime Factorization:
- For 24:
![\[ 24 = 2^3 \times 3^1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-377ed7bafb82a7fa850c70a7c2b06a60_l3.png "Rendered by QuickLaTeX.com")
- For 36:
![\[ 36 = 2^2 \times 3^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-30f64b9e306132db342ed06ca285158a_l3.png "Rendered by QuickLaTeX.com")
2. Identify Common Factors: The common prime factors are 2 and 3.
3. Choose the Lowest Powers:
- For 2: The lowest power is
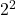. - For 3: The lowest power is
.
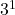4. Multiply the Common Factors:
![\[ HCF = 2^2 \times 3^1 = 4 \times 3 = 12 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9e561c4165881b2caffd7f9efd173306_l3.png "Rendered by QuickLaTeX.com")
Thus, the HCF of 24 and 36 is 12.
Finding LCM Using Prime Factorization
To find the LCM of two or more numbers using prime factorization, follow these steps:
1. Find the Prime Factorization: Determine the prime factorization of each number.
2. Identify All Factors: List all the prime factors that appear in the factorizations.
3. Choose the Highest Powers: For each prime factor, choose the highest power that appears in any of the factorizations.
4. Multiply the Factors: Multiply these factors together to get the LCM.
Illustrative Example
Let’s find the LCM of 24 and 36.
1. Prime Factorization:
- For 24:
- For 36:
2. Identify All Factors: The prime factors are 2 and 3.
3. Choose the Highest Powers:
- For 2: The highest power is
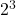. - For 3: The highest power is
.
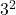4. Multiply the Factors:
![\[ LCM = 2^3 \times 3^2 = 8 \times 9 = 72 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7abe1fcd232948bfc0669c85093fb404_l3.png "Rendered by QuickLaTeX.com")
Thus, the LCM of 24 and 36 is 72.
Relationship Between HCF and LCM
There is a fundamental relationship between the HCF and LCM of two numbers, which can be expressed as:
![\[ \text{HCF} \times \text{LCM} = a \times b \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-1aa98b2644facae495ae6dd7420c8a8d_l3.png "Rendered by QuickLaTeX.com")
where 
and 
are the two numbers.
Illustrative Explanation
To illustrate this relationship, consider the numbers 24 and 36:
- We found that:
- HCF = 12
- LCM = 72
Now, let’s verify the relationship:
![\[ \text{HCF} \times \text{LCM} = 12 \times 72 = 864 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-6f3c1a9b16a35c05f43b6ecad917aa4e_l3.png "Rendered by QuickLaTeX.com")
And:
![\[ a \times b = 24 \times 36 = 864 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9979e5df2cac60769c8926a843a60335_l3.png "Rendered by QuickLaTeX.com")
This confirms that the relationship holds true.
Applications of HCF and LCM
Understanding the HCF and LCM has several practical applications:
1. Simplifying Fractions: The HCF is used to simplify fractions to their lowest terms. For example, to simplify 
, you can divide both the numerator and denominator by their HCF, which is 12:
![\[ \frac{24 \div 12}{36 \div 12} = \frac{2}{3} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9873cb69044c1a7a08f7b5288fa2d591_l3.png "Rendered by QuickLaTeX.com")
2. Finding Common Denominators: The LCM is used to find a common denominator when adding or subtracting fractions. For example, to add 
and 
, you can find the LCM of 4 and 6, which is 12, and convert both fractions:
![\[ \frac{1}{4} = \frac{3}{12}, \quad \frac{1}{6} = \frac{2}{12} \quad \Rightarrow \quad \frac{3}{12} + \frac{2}{12} = \frac{5}{12} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e63641a3c6901d8c49de7a844ed9d969_l3.png "Rendered by QuickLaTeX.com")
3. Problem Solving in Real Life: HCF and LCM are used in various real-life scenarios, such as scheduling events, distributing items evenly, and solving problems involving ratios and proportions.
Illustrative Explanation
Imagine a group of friends planning a party. They want to buy drinks in packs of 4 and snacks in packs of 6. To ensure they have enough for everyone without leftovers, they can use the LCM to determine the smallest number of packs they need to buy. By finding the LCM of 4 and 6 (which is 12), they can buy 3 packs of drinks and 2 packs of snacks, ensuring that everything is evenly distributed.
Conclusion
In conclusion, the prime factorization of the Highest Common Factor (HCF) and the Lowest Common Multiple (LCM) is a vital concept in mathematics that helps us understand the relationships between numbers. By breaking down numbers into their prime factors, we can easily find the HCF and LCM, which have numerous applications in simplifying fractions, finding common denominators, and solving real-life problems. The relationship between HCF and LCM further emphasizes the interconnectedness of these concepts, making them essential tools in both theoretical and practical mathematics. Understanding these principles not only enhances our mathematical skills but also equips us with the knowledge to tackle a wide range of problems in everyday life.