In statistics, the concepts of mean, median, and mode are fundamental measures of central tendency that provide insights into the distribution of data. Understanding the relationship between these three measures is crucial for analyzing data sets effectively. This article will delve into the definitions, properties, calculations, and relationships between mean, median, and mode, along with illustrative explanations to enhance comprehension.
1. Definitions
A. Mean
The mean, often referred to as the average, is calculated by summing all the values in a data set and dividing by the number of values. It is a measure that represents the central point of a data set.
Mathematical Representation:
For a data set with 
values 
:
![\[ \text{Mean} = \frac{x_1 + x_2 + x_3 + \ldots + x_n}{n} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-81207cd96b75d19a55cbaae281ee17cd_l3.png "Rendered by QuickLaTeX.com")
Illustrative Example:
Consider the data set: 
.
1. Sum of values: 
2. Number of values: 
3. Mean:
![\[ \text{Mean} = \frac{26}{5} = 5.2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-c9ef2d0f8d5c3bf406a3312f6068b4ec_l3.png "Rendered by QuickLaTeX.com")
B. Median
The median is the middle value of a data set when the values are arranged in ascending or descending order. If the number of values is odd, the median is the middle number. If the number of values is even, the median is the average of the two middle numbers.
Mathematical Representation:
1. Odd number of values: If is odd, the median is:
![\[ \text{Median} = x_{\left(\frac{n+1}{2}\right)} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f7a9c32aefed4dd8d0d0ac2056925f77_l3.png "Rendered by QuickLaTeX.com")
2. Even number of values: If is even, the median is:
![\[ \text{Median} = \frac{x_{\left(\frac{n}{2}\right)} + x_{\left(\frac{n}{2} + 1\right)}}{2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-94e4d7a955ca33a1e93734c842094dfb_l3.png "Rendered by QuickLaTeX.com")
Illustrative Example:
Using the same data set :
1. Arrange in ascending order: 
2. Middle value: The middle value (3rd value) is .
3. Median:
![\[ \text{Median} = 5 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7010e16f69d44d2c1b36c5e2e0a1b031_l3.png "Rendered by QuickLaTeX.com")
C. Mode
The mode is the value that appears most frequently in a data set. A data set may have one mode, more than one mode (bimodal or multimodal), or no mode at all if all values occur with the same frequency.
Illustrative Example:
Consider the data set: 
.
1. Frequency of values:
– 
: 1 time
– 
: 2 times
– 
: 1 time
– 
: 3 times
2. Mode: The value that appears most frequently is .
![\[ \text{Mode} = 4 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-006f17a847dc3ac96899d823bed23399_l3.png "Rendered by QuickLaTeX.com")
2. Properties of Mean, Median, and Mode
A. Mean:
- Sensitive to extreme values (outliers). A single outlier can significantly affect the mean.
- Useful for data sets with a normal distribution.
B. Median:
- Not affected by outliers, making it a better measure of central tendency for skewed distributions.
- Represents the 50th percentile of the data.
C. Mode:
- Can be used with nominal data (categorical data) where mean and median cannot be calculated.
- Useful for understanding the most common value in a data set.
3. Relationship Between Mean, Median, and Mode
The relationship between mean, median, and mode can vary depending on the distribution of the data. Here are some key points regarding their relationships:
A. Symmetrical Distribution:
In a perfectly symmetrical distribution (like a normal distribution), the mean, median, and mode are all equal.
![\[ \text{Mean} = \text{Median} = \text{Mode} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-5023a2f00e7487684962da18fd6fefb0_l3.png "Rendered by QuickLaTeX.com")
Illustrative Example:
For a normal distribution, consider the data set: 
.
- Mean:
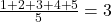
- Median: Middle value is
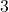
- Mode: No repeating values, so no mode, but if we had 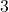repeated, it would still be .
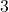B. Skewed Distribution:
In skewed distributions, the mean, median, and mode will differ:
1. Positively Skewed Distribution (right-skewed):
– Mode < Median < Mean
In this case, the tail on the right side of the distribution pulls the mean to the right.
Illustrative Example:
Consider the data set: 
.
- Mean:
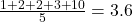
- Median: Middle value is
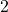
- Mode: Most frequent value is
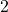
Here, 
.
2. Negatively Skewed Distribution (left-skewed):
– Mean < Median < Mode
In this case, the tail on the left side of the distribution pulls the mean to the left.
Illustrative Example:
Consider the data set: 
.
- Mean:
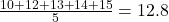
- Median: Middle value is
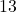
- Mode: No repeating values, so no mode.
Here, 
.
4. Applications of Mean, Median, and Mode
Understanding the relationship between mean, median, and mode is essential in various fields:
A. Statistics:
These measures are used to summarize data sets, making it easier to understand and interpret data.
B. Economics:
Mean income, median household income, and mode of product sales are crucial for economic analysis and policy-making.
C. Psychology:
In psychological research, these measures help summarize test scores, survey results, and behavioral data.
D. Education:
Mean, median, and mode are used to analyze student performance, test scores, and grading distributions.
5. Conclusion
The mean, median, and mode are essential statistical measures that provide valuable insights into data sets. Understanding their definitions, calculations, properties, and relationships is crucial for effective data analysis.
Key Takeaways:
- The mean is the average of a data set, sensitive to outliers.
- The median is the middle value, robust against outliers.
- The mode is the most frequently occurring value, applicable to categorical data.
- In symmetrical distributions, mean, median, and mode are equal; in skewed distributions, they differ in specific ways.
By mastering these concepts, individuals can enhance their statistical literacy and apply these principles effectively in various fields, leading to better data-driven decision-making and analysis.