Resistors are fundamental components in electrical and electronic circuits, used to limit the flow of electric current, divide voltages, and protect sensitive components from excessive current. Understanding how resistors behave in different configurations—specifically in series and parallel—is crucial for designing and analyzing circuits. This article aims to provide an exhaustive overview of resistors in series and parallel configurations, detailing their definitions, characteristics, calculations, and applications, along with illustrative explanations of each concept.
Understanding Resistors
1. Definition of a Resistor
A resistor is a passive electrical component that opposes the flow of electric current, resulting in a voltage drop across its terminals. The resistance of a resistor is measured in ohms (Ω), and it is defined by Ohm’s Law, which states:
![]()
Where:
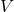 is the voltage across the resistor,
is the voltage across the resistor,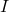 is the current flowing through the resistor,
is the current flowing through the resistor,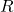 is the resistance.
is the resistance.- Illustrative Explanation: Imagine a narrow pipe carrying water. The pipe’s narrowness represents resistance; the narrower the pipe, the harder it is for water to flow through. Just as a narrow pipe restricts water flow, a resistor limits the flow of electric current in a circuit.
Resistors in Series Configuration
2. Definition of Series Configuration
In a series configuration, resistors are connected end-to-end in a single path for the electric current to flow. The same current flows through each resistor, and the total resistance of the circuit is the sum of the individual resistances.
- Illustrative Explanation: Picture a line of people passing a ball from one to another. Each person represents a resistor, and the ball represents the electric current. The ball can only move through the line one person at a time, just as current flows through each resistor in series.
3. Characteristics of Resistors in Series
- Current: The current flowing through each resistor in a series circuit is the same. This is because there is only one path for the current to take.
- Voltage: The total voltage across the series circuit is the sum of the voltages across each resistor. According to Ohm’s Law, the voltage drop across each resistor can be calculated as:
![]()
Where:
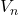 is the voltage across the nth resistor,
is the voltage across the nth resistor,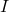 is the current through the circuit,
is the current through the circuit,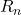 is the resistance of the nth resistor.
is the resistance of the nth resistor.- Total Resistance: The total resistance (
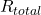 ) in a series circuit is given by the formula:
) in a series circuit is given by the formula:
![]()
Where ![]() are the individual resistances.
are the individual resistances.
- Illustrative Explanation: If you have three resistors in series with resistances of
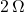 ,
, 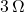 , and
, and 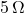 , the total resistance would be:
, the total resistance would be:
![]()
Just as the total resistance increases with each additional resistor, the total voltage drop across the series circuit is the sum of the individual voltage drops.
4. Calculating Total Resistance in Series
To calculate the total resistance in a series circuit, simply add the resistance values of all resistors:
Example: If you have three resistors with values ![]() ,
, ![]() , and
, and ![]() :
:
![]()
- Illustrative Explanation: Just as stacking three books increases the total height, adding resistors in series increases the total resistance.
Resistors in Parallel Configuration
5. Definition of Parallel Configuration
In a parallel configuration, resistors are connected across the same two points, creating multiple paths for the electric current to flow. The voltage across each resistor is the same, but the current can vary depending on the resistance of each branch.
- Illustrative Explanation: Imagine a road with multiple lanes. Cars can choose any lane to travel, just as electric current can flow through multiple resistors in parallel. Each lane represents a different path for the current.
6. Characteristics of Resistors in Parallel
- Voltage: The voltage across each resistor in a parallel circuit is the same and is equal to the total voltage supplied by the source.
- Current: The total current flowing through the circuit is the sum of the currents through each resistor. According to Kirchhoff’s Current Law, the total current (
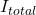 ) can be expressed as:
) can be expressed as:
![]()
Where ![]() are the currents through each resistor.
are the currents through each resistor.
- Total Resistance: The total resistance (
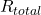 ) in a parallel circuit can be calculated using the formula:
) in a parallel circuit can be calculated using the formula:
![]()
Where ![]() are the individual resistances.
are the individual resistances.
- Illustrative Explanation: If you have three resistors in parallel with resistances of
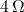 ,
, 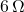 , and
, and 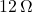 , the total resistance can be calculated as follows:
, the total resistance can be calculated as follows:
![]()
Finding a common denominator (which is 12), we get:
![]()
Thus, ![]() .
.
Just as having multiple lanes allows more cars to travel simultaneously, having resistors in parallel reduces the total resistance, allowing more current to flow.
7. Calculating Total Resistance in Parallel
To calculate the total resistance in a parallel circuit, use the reciprocal formula mentioned above.
Example: If you have three resistors with values ![]() ,
, ![]() , and
, and ![]() :
:
![]()
Finding a common denominator (which is 12):
![]()
Thus, ![]() .
.
- Illustrative Explanation: Just as multiple paths allow more cars to travel at once, multiple resistors in parallel allow more current to flow, resulting in a lower total resistance.
Applications of Resistors in Series and Parallel
1. Voltage Dividers
Resistors in series are often used in voltage divider circuits, where the total voltage is divided among the resistors. This is useful for obtaining a specific voltage level from a higher voltage source.
- Illustrative Explanation: Imagine a water tank with multiple outlets at different heights. Each outlet allows water to flow out at a different rate, just as a voltage divider provides different voltage levels.
2. Current Dividers
Resistors in parallel are used in current divider circuits, where the total current is divided among the parallel branches. This is useful for distributing current to multiple loads.
- Illustrative Explanation: Think of a river splitting into multiple streams. Each stream carries a portion of the water, just as a current divider distributes current among parallel resistors.
3. Load Balancing
In power distribution systems, resistors can be used in series or parallel configurations to balance loads and ensure that no single component is overloaded.
- Illustrative Explanation: Imagine a team of workers sharing a heavy load. By distributing the weight evenly, no single worker becomes overwhelmed, just as resistors help balance electrical loads.
4. Signal Conditioning
In electronic circuits, resistors are used in both series and parallel configurations to condition signals, filter noise, and set gain levels in amplifiers.
- Illustrative Explanation: Consider a musician tuning their instrument. By adjusting the tension of the strings, they can produce the desired sound. Similarly, resistors help fine-tune electrical signals for optimal performance.
Conclusion
In conclusion, understanding resistors in series and parallel configurations is essential for analyzing and designing electrical circuits. By exploring their definitions, characteristics, calculations, and applications, we can appreciate the significance of these configurations in various fields, from electronics and engineering to power distribution and signal processing. The study of resistors not only deepens our understanding of electrical principles but also highlights the importance of precise measurements and configurations in achieving desired outcomes in circuit design. Whether in series or parallel, resistors play a crucial role in shaping the behavior of electrical circuits, making them indispensable components in modern technology. Understanding how to effectively use resistors in different configurations is vital for anyone working with electrical systems, paving the way for innovations that can benefit society as a whole.