The Schrödinger Wave Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes over time. It is a cornerstone of quantum theory, providing a mathematical framework for understanding the behavior of particles at the atomic and subatomic levels. This article will provide a detailed exploration of the Schrödinger Wave Equation, including its formulation, significance, interpretations, and illustrative explanations to enhance understanding.
1. Introduction to Quantum Mechanics
Before delving into the Schrödinger Wave Equation, it is essential to understand the context of quantum mechanics. Quantum mechanics is the branch of physics that deals with the behavior of matter and energy at very small scales, such as atoms and subatomic particles. Unlike classical mechanics, which describes the motion of macroscopic objects, quantum mechanics introduces concepts such as wave-particle duality, uncertainty, and superposition.
A. Wave-Particle Duality
Wave-particle duality is the concept that particles, such as electrons and photons, exhibit both wave-like and particle-like properties. This duality is fundamental to understanding quantum phenomena.
Illustrative Explanation: Imagine a beach ball (particle) rolling along the sand. As it moves, it creates ripples in the water (wave). Just as the ball can be seen as both a solid object and a source of waves, particles in quantum mechanics can behave like both particles and waves.
2. The Schrödinger Wave Equation
The Schrödinger Wave Equation was formulated by the Austrian physicist Erwin Schrödinger in 1925. It describes how the quantum state of a system evolves over time and is expressed in two primary forms: the time-dependent Schrödinger equation and the time-independent Schrödinger equation.
A. Time-Dependent Schrödinger Equation
The time-dependent Schrödinger equation describes how the wave function of a quantum system changes with time. It is given by:
![\[ i\hbar \frac{\partial \Psi(\mathbf{r}, t)}{\partial t} = \hat{H} \Psi(\mathbf{r}, t) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-963008150d9526aa07b0a378704718c4_l3.png "Rendered by QuickLaTeX.com")
Where:
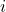is the imaginary unit.
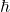(h-bar) is the reduced Planck’s constant.
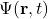is the wave function of the system, which contains all the information about the system’s state.
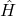is the Hamiltonian operator, representing the total energy of the system.
Illustrative Explanation: Think of the wave function 
as a detailed map of a landscape (the quantum state) that changes over time. The time-dependent Schrödinger equation describes how this map evolves, similar to how weather patterns change across a geographical area.
B. Time-Independent Schrödinger Equation
The time-independent Schrödinger equation is used for systems in a stationary state, where the energy does not change with time. It is given by:
![\[ \hat{H} \Psi(\mathbf{r}) = E \Psi(\mathbf{r}) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a31e33725c6fb3305e0706f68f6721b0_l3.png "Rendered by QuickLaTeX.com")
Where:
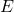is the total energy of the system.
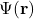is the spatial wave function, which describes the probability distribution of finding a particle in a given position.
Illustrative Explanation: Imagine a still pond where the surface reflects the surrounding landscape. The time-independent Schrödinger equation captures the “snapshot” of the wave function at a specific moment, showing where the particle is likely to be found, much like how the reflection shows the scenery above the water.
3. Significance of the Schrödinger Wave Equation
The Schrödinger Wave Equation is significant for several reasons:
A. Foundation of Quantum Mechanics
The equation provides a mathematical framework for understanding quantum systems, allowing physicists to predict the behavior of particles and their interactions.
Illustrative Explanation: Consider the Schrödinger equation as the blueprint for a complex building (quantum system). Just as architects use blueprints to design and construct buildings, physicists use the equation to understand and predict the behavior of quantum systems.
B. Wave Function and Probability
The wave function contains all the information about a quantum system, and its square modulus 
gives the probability density of finding a particle in a particular location. This probabilistic interpretation is a departure from classical determinism.
Illustrative Explanation: Imagine throwing a handful of darts at a dartboard. The wave function represents the distribution of where the darts might land. The more densely packed areas on the board correspond to higher probabilities of finding a dart, similar to how indicates where a particle is likely to be found.
C. Quantum Tunneling
The Schrödinger Wave Equation allows for the phenomenon of quantum tunneling, where particles can pass through potential barriers that they classically should not be able to cross. This has profound implications in fields such as nuclear physics and semiconductor technology.
Illustrative Explanation: Picture a ball rolling toward a hill (potential barrier). In classical physics, if the ball doesn’t have enough energy to climb the hill, it will roll back. However, in quantum mechanics, the ball can “tunnel” through the hill, appearing on the other side, much like how particles can pass through barriers in quantum systems.
4. Interpretations of the Schrödinger Wave Equation
Several interpretations of the Schrödinger Wave Equation exist, each providing a different perspective on the nature of quantum mechanics:
A. Copenhagen Interpretation
The Copenhagen interpretation, proposed by Niels Bohr and Werner Heisenberg, posits that the wave function represents our knowledge of a system rather than a physical reality. Upon measurement, the wave function collapses to a definite state.
Illustrative Explanation: Imagine a box containing a cat that is both alive and dead (Schrödinger’s cat thought experiment) until you open the box to check. The act of observation collapses the wave function, determining the cat’s state, similar to how measurements affect quantum systems.
B. Many-Worlds Interpretation
The many-worlds interpretation, proposed by Hugh Everett III, suggests that all possible outcomes of a quantum event occur in separate, branching universes. The wave function never collapses; instead, it evolves into a superposition of all possible states.
Illustrative Explanation: Picture a tree with branches representing different outcomes of a decision. Each branch leads to a different reality, just as the many-worlds interpretation posits that every possible outcome of a quantum event exists in its own universe.
C. Pilot-Wave Theory
Pilot-wave theory, also known as de Broglie-Bohm theory, introduces the idea of a “pilot wave” guiding particles along deterministic paths. This interpretation maintains that particles have definite positions and velocities, contrary to the probabilistic nature of other interpretations.
Illustrative Explanation: Imagine a boat (particle) being guided by a river current (pilot wave). The current directs the boat’s path, allowing it to move through the water with a specific trajectory, similar to how the pilot wave influences the behavior of particles.
5. Applications of the Schrödinger Wave Equation
The Schrödinger Wave Equation has numerous applications across various fields:
A. Quantum Chemistry
In quantum chemistry, the Schrödinger equation is used to calculate the electronic structure of atoms and molecules, helping to predict chemical properties and reactions.
Illustrative Explanation: Think of the Schrödinger equation as a recipe that provides the necessary ingredients and steps to understand how atoms bond and interact, much like a chef following a recipe to create a dish.
B. Solid-State Physics
The equation is essential in solid-state physics for understanding the behavior of electrons in solids, leading to the development of semiconductors, superconductors, and other materials.
Illustrative Explanation: Imagine a city with a complex network of roads (electrons) and buildings (atoms). The Schrödinger equation helps map out how the roads connect and how traffic flows, similar to how it describes electron behavior in materials.
C. Quantum Computing
Quantum computing relies on the principles of quantum mechanics, including the Schrödinger equation, to develop new computational methods that can solve complex problems more efficiently than classical computers.
Illustrative Explanation: Picture a traditional computer as a library with books arranged in a specific order. A quantum computer, guided by the Schrödinger equation, can explore multiple books simultaneously, allowing for faster information retrieval and problem-solving.
6. Conclusion
In summary, the Schrödinger Wave Equation is a fundamental equation in quantum mechanics that describes the evolution of quantum states over time. Its formulation, significance, and various interpretations provide a comprehensive understanding of the behavior of particles at the quantum level. By grasping the principles of the Schrödinger Wave Equation, we can appreciate its profound implications for fields such as quantum chemistry, solid-state physics, and quantum computing. As our understanding of quantum mechanics continues to evolve, the Schrödinger Wave Equation will remain a cornerstone of theoretical physics, guiding future discoveries and innovations in the realm of the microscopic world. Understanding this equation not only enhances our knowledge of the universe but also empowers us to engage with the technologies that shape our modern lives.