The square root is a fundamental mathematical concept that plays a crucial role in various fields, including algebra, geometry, and calculus. It is the inverse operation of squaring a number and is essential for solving equations, understanding geometric properties, and performing calculations in real-world applications. This article aims to provide an exhaustive overview of square roots, including their definition, properties, methods of calculation, applications, and illustrative explanations for each concept.
1. Definition of Square Root
1.1. What is a Square Root?
The square root of a number ![]() is a value
is a value ![]() such that when
such that when ![]() is multiplied by itself, it equals
is multiplied by itself, it equals ![]() . In mathematical notation, this is expressed as:
. In mathematical notation, this is expressed as:
![]()
Illustrative Explanation: For example, the square root of ![]() is
is ![]() because
because ![]() . Thus, we can write:
. Thus, we can write:
![]()
1.2. Notation
The square root is denoted by the radical symbol ![]() . The number under the radical is called the radicand. For instance, in
. The number under the radical is called the radicand. For instance, in ![]() ,
, ![]() is the radicand.
is the radicand.
2. Properties of Square Roots
2.1. Non-Negative Results
The square root of a non-negative number is always non-negative. This means that ![]() for any
for any ![]() .
.
Illustrative Explanation: The square root of ![]() is
is ![]() , and the square root of
, and the square root of ![]() is
is ![]() . However, the square root of a negative number is not defined in the set of real numbers; it leads to complex numbers.
. However, the square root of a negative number is not defined in the set of real numbers; it leads to complex numbers.
2.2. Square Roots of Perfect Squares
A perfect square is a number that is the square of an integer. The square root of a perfect square is always an integer.
Illustrative Explanation: The perfect squares ![]() have square roots
have square roots ![]() respectively. Thus:
respectively. Thus:
![]()
2.3. Product Property of Square Roots
The square root of a product of two numbers is equal to the product of their square roots:
![]()
Illustrative Explanation: For example, ![]() .
.
2.4. Quotient Property of Square Roots
The square root of a quotient of two numbers is equal to the quotient of their square roots:
![]()
Illustrative Explanation: For instance, ![]() .
.
2.5. Square Root of Zero
The square root of zero is zero:
![]()
Illustrative Explanation: This is because ![]() .
.
3. Calculating Square Roots
3.1. Finding Square Roots of Perfect Squares
For perfect squares, finding the square root is straightforward. You can simply identify the integer that, when squared, gives the perfect square.
Illustrative Explanation: To find ![]() , recognize that
, recognize that ![]() , so
, so ![]() .
.
3.2. Estimating Square Roots of Non-Perfect Squares
For non-perfect squares, you can estimate the square root by finding the two perfect squares it lies between.
Illustrative Explanation: To estimate ![]() :
:
- Identify that
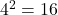 and
and 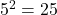 .
. - Thus,
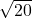 is between
is between 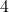 and
and 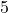 .
.
3.3. Using the Long Division Method
The long division method can be used to find square roots of non-perfect squares to a desired degree of accuracy. This method involves a systematic approach to divide and find the square root.
Illustrative Explanation: To find ![]() using the long division method:
using the long division method:
1. Pair the digits of ![]() from right to left (20).
from right to left (20).
2. Find the largest integer whose square is less than or equal to ![]() (which is
(which is ![]() ).
).
3. Subtract ![]() from
from ![]() to get
to get ![]() .
.
4. Bring down a pair of zeros, making it ![]() .
.
5. Double the current quotient (![]() ) to get
) to get ![]() and find a digit
and find a digit ![]() such that
such that ![]() is less than or equal to
is less than or equal to ![]() .
.
6. Continue this process to refine the estimate.
3.4. Using a Calculator
For practical purposes, calculators can be used to find square roots quickly and accurately. Most scientific calculators have a square root function.
Illustrative Explanation: Simply input ![]() and press the square root button to get approximately
and press the square root button to get approximately ![]() .
.
4. Applications of Square Roots
4.1. Geometry
Square roots are frequently used in geometry, particularly in calculating the lengths of sides in right triangles using the Pythagorean theorem:
![]()
where ![]() is the hypotenuse, and
is the hypotenuse, and ![]() and
and ![]() are the other two sides.
are the other two sides.
Illustrative Explanation: If a right triangle has legs measuring ![]() units and
units and ![]() units, the length of the hypotenuse is:
units, the length of the hypotenuse is:
![]()
4.2. Physics
In physics, square roots are used in various formulas, including those related to motion, energy, and wave properties. For example, the formula for the period of a simple pendulum involves the square root of the length of the pendulum.
Illustrative Explanation: The period ![]() of a pendulum is given by:
of a pendulum is given by:
![Rendered by QuickLaTeX.com \[ T = 2\pi \sqrt{\frac{L}{g}} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-3316850bc8981bec3bbb727f9c468cae_l3.png)
where ![]() is the length of the pendulum and
is the length of the pendulum and ![]() is the acceleration due to gravity.
is the acceleration due to gravity.
4.3. Statistics
In statistics, the square root is used in calculating the standard deviation, which measures the amount of variation or dispersion in a set of values.
Illustrative Explanation: The standard deviation ![]() is calculated as:
is calculated as:
![]()
where ![]() represents each value,
represents each value, ![]() is the mean, and
is the mean, and ![]() is the number of values.
is the number of values.
4.4. Finance
In finance, square roots are used in various calculations, including those related to risk assessment and investment returns. The volatility of an investment is often measured using the standard deviation, which involves square roots.
Illustrative Explanation: If an investment has a standard deviation of ![]() , this indicates the average deviation from the expected return, helping investors assess risk.
, this indicates the average deviation from the expected return, helping investors assess risk.
5. Limitations of Square Roots
5.1. Negative Radicands
The square root of a negative number is not defined in the set of real numbers. Instead, it leads to complex numbers, which include imaginary units.
Illustrative Explanation: The expression ![]() is not a real number. Instead, it can be expressed as
is not a real number. Instead, it can be expressed as ![]() , where
, where ![]() is the imaginary unit.
is the imaginary unit.
5.2. Complexity in Higher Dimensions
In higher-dimensional geometry, the concept of square roots can become more complex, particularly when dealing with vectors and matrices.
5.3. Misinterpretation of Properties
Students may sometimes confuse the properties of square roots with those of other mathematical operations, leading to errors in calculations.
Conclusion
In conclusion, the square root is a fundamental mathematical concept that is essential for understanding various mathematical principles and applications. Its definition, properties, methods of calculation, and applications in geometry, physics, statistics, and finance highlight its significance in both theoretical and practical contexts. By mastering the concept of square roots, students and enthusiasts of mathematics can enhance their problem-solving skills and deepen their understanding of mathematical relationships. As we continue to explore the world of mathematics, the study of square roots will remain a vital part of our understanding of numbers and their properties, paving the way for more advanced mathematical concepts and applications.