The Stefan-Boltzmann Law is a fundamental principle in thermodynamics and physics that describes how the total energy radiated by a black body is related to its temperature. This law has profound implications in various fields, including astrophysics, climate science, and engineering. This article provides an in-depth examination of the Stefan-Boltzmann Law, including its definition, mathematical formulation, significance, applications, and illustrative explanations of each concept.
—
1. Definition of the Stefan-Boltzmann Law
The Stefan-Boltzmann Law states that the total energy radiated per unit surface area of a black body per unit time (also known as the radiant energy flux) is directly proportional to the fourth power of its absolute temperature (T). Mathematically, the law is expressed as:
![\[ E = \sigma T^4 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f8f6282fd0eb5173d7c43019a3df1ed6_l3.png "Rendered by QuickLaTeX.com")
Where:
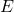is the radiant energy flux (in watts per square meter, W/m²),
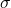is the Stefan-Boltzmann constant (
),
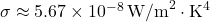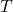is the absolute temperature of the black body (in kelvins, K).
Illustrative Explanation:
Imagine a perfect black body, such as a blackened metal sphere, heated to a certain temperature. As you increase the temperature of the sphere, it begins to glow. The Stefan-Boltzmann Law tells us that the amount of energy it radiates increases dramatically as the temperature rises. For instance, if you double the temperature of the sphere, the energy it radiates increases by a factor of 16 (since 
).
—
2. Understanding Black Bodies
A black body is an idealized physical object that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. It is also a perfect emitter of radiation, meaning it emits energy at the maximum possible rate for any given temperature. While no perfect black body exists in reality, many materials approximate this behavior closely.
Illustrative Explanation:
Consider a black-painted object placed in sunlight. The black surface absorbs most of the sunlight that hits it, making it warmer than a white or reflective surface. This behavior is similar to that of a theoretical black body, which absorbs all radiation and, as a result, reaches a higher temperature.
—
3. The Stefan-Boltzmann Constant
The Stefan-Boltzmann constant () is a fundamental physical constant that plays a crucial role in the Stefan-Boltzmann Law. Its value is approximately 
. This constant allows us to convert the temperature of a black body into the total energy it radiates.
Illustrative Explanation:
To understand the significance of the Stefan-Boltzmann constant, consider a black body at a temperature of 300 K (approximately room temperature). Using the Stefan-Boltzmann Law, we can calculate the radiant energy flux:
![\[ E = \sigma T^4 = (5.67 \times 10^{-8} \, \text{W/m}^2 \cdot \text{K}^4) \times (300 \, \text{K})^4 \approx 7.63 \times 10^4 \, \text{W/m}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d5c67e5d312bd240d5ddf421ab575d1f_l3.png "Rendered by QuickLaTeX.com")
This calculation shows that a black body at room temperature radiates a significant amount of energy.
—
4. Implications of the Stefan-Boltzmann Law
The Stefan-Boltzmann Law has several important implications in various fields:
4.1 Astrophysics
In astrophysics, the Stefan-Boltzmann Law is used to estimate the luminosity (total energy output) of stars. By measuring the temperature of a star and applying the law, astronomers can determine how much energy the star emits.
Illustrative Explanation:
Consider a star with a surface temperature of 5,800 K (similar to the Sun). By applying the Stefan-Boltzmann Law, astronomers can calculate the total energy radiated by the star per unit area and then multiply it by the star’s surface area to find its total luminosity. This information is crucial for understanding the star’s life cycle and its impact on surrounding celestial bodies.
4.2 Climate Science
The Stefan-Boltzmann Law is fundamental in climate science, particularly in understanding the Earth’s energy balance. The Earth absorbs solar radiation and re-emits energy as infrared radiation. The law helps scientists model how changes in temperature affect the amount of energy radiated back into space.
Illustrative Explanation:
When the Earth’s average temperature increases due to greenhouse gas emissions, the Stefan-Boltzmann Law indicates that the amount of energy radiated into space will also increase. However, if the energy absorbed exceeds the energy radiated, the Earth will continue to warm, leading to climate change.
4.3 Engineering Applications
In engineering, the Stefan-Boltzmann Law is applied in the design of thermal systems, such as radiators, heat exchangers, and thermal insulation. Understanding how materials emit and absorb radiation helps engineers optimize energy efficiency.
Illustrative Explanation:
In designing a radiator for a heating system, engineers can use the Stefan-Boltzmann Law to determine how much heat the radiator will emit at a given temperature. By selecting materials with appropriate emissivity (the efficiency of a surface in emitting energy), they can enhance the radiator’s performance.
—
5. Emissivity and Real Surfaces
While the Stefan-Boltzmann Law applies to ideal black bodies, real surfaces have varying emissivities, which measure how effectively a surface emits thermal radiation compared to a black body. Emissivity (
) is a dimensionless quantity ranging from 0 to 1, where 1 represents a perfect black body.
Illustrative Explanation:
Consider two surfaces: a polished metal surface with an emissivity of 0.1 and a rough black surface with an emissivity of 0.95. If both surfaces are at the same temperature, the rough black surface will emit significantly more thermal radiation than the polished metal surface. The Stefan-Boltzmann Law can be modified to account for emissivity:
![\[ E = \epsilon \sigma T^4 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-19c6ce259924e4d389871a0dc9558ba5_l3.png "Rendered by QuickLaTeX.com")
This equation allows us to calculate the radiant energy flux for real surfaces.
—
6. Applications of the Stefan-Boltzmann Law
The Stefan-Boltzmann Law has a wide range of applications across various fields:
6.1 Thermal Imaging
In thermal imaging, the Stefan-Boltzmann Law is used to analyze the thermal radiation emitted by objects. Thermal cameras detect infrared radiation and convert it into images, allowing for temperature measurements and heat distribution analysis.
Illustrative Explanation:
A thermal camera can be used to identify heat leaks in a building. By measuring the infrared radiation emitted from the building’s surfaces, the camera can create a thermal image that highlights areas of heat loss, helping homeowners improve energy efficiency.
6.2 Space Exploration
In space exploration, the Stefan-Boltzmann Law is essential for understanding the thermal environment of spacecraft and planetary bodies. Engineers use the law to design thermal control systems that maintain optimal temperatures for instruments and equipment.
Illustrative Explanation:
When designing a spacecraft for a mission to Mars, engineers must consider the temperature fluctuations in space. By applying the Stefan-Boltzmann Law, they can calculate how much heat the spacecraft will radiate and ensure that it remains within safe operating temperatures.
6.3 HVAC Systems
In heating, ventilation, and air conditioning (HVAC) systems, the Stefan-Boltzmann Law helps engineers design efficient heating and cooling systems. By understanding how surfaces emit and absorb thermal radiation, they can optimize energy use in buildings.
Illustrative Explanation:
In a commercial building, HVAC engineers can use the Stefan-Boltzmann Law to calculate the heat loss through windows and walls. By selecting appropriate insulation materials and designing the HVAC system accordingly, they can minimize energy consumption and maintain comfortable indoor temperatures.
—
Conclusion
The Stefan-Boltzmann Law is a fundamental principle that describes the relationship between temperature and radiant energy emission. Its implications extend across various fields, from astrophysics and climate science to engineering and thermal imaging. By understanding the Stefan-Boltzmann Law, we gain valuable insights into the behavior of thermal radiation and its applications in the real world. This knowledge is essential for addressing challenges related to energy efficiency, climate change, and technological advancements, making the Stefan-Boltzmann Law a cornerstone of modern physics and engineering.