Tangents to an Ellipse: A Comprehensive Exploration

An ellipse is a closed curve that results from the intersection of a cone with a plane that is not parallel to the base of the cone. It is a fundamental shape in mathematics and physics, characterized by its two focal points, major and minor axes, and a variety of properties that make it unique. Understanding tangents to an ellipse is crucial in various fields, including geometry, physics, engineering, and computer graphics. This article aims to provide an exhaustive overview of tangents to an ellipse, detailing their definitions, mathematical properties, and practical applications, along with illustrative explanations of each concept.

Understanding the Ellipse

1. Definition of an Ellipse

An ellipse can be defined mathematically as the set of all points in a plane such that the sum of the distances from two fixed points (the foci) is constant. The standard equation of an ellipse centered at the origin with a horizontal major axis is given by:

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Where:

$a$ is the semi-major axis (the distance from the center to the farthest point on the ellipse),
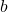$b$ is the semi-minor axis (the distance from the center to the closest point on the ellipse).
Illustrative Explanation: Imagine a stretched rubber band. If you hold two points fixed and stretch the band around them, the shape formed is an ellipse. The distance from any point on the band to the two fixed points remains constant, illustrating the definition of an ellipse.

2. Properties of an Ellipse

Ellipses have several important properties:

Foci: The two fixed points inside the ellipse. The distance from any point on the ellipse to the foci has a constant sum.
Axes: The major axis is the longest diameter of the ellipse, while the minor axis is the shortest.
Eccentricity: A measure of how “stretched” the ellipse is, defined as 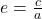$e = \frac{c}{a}$ , where $c$ is the distance from the center to a focus.
Illustrative Explanation: Consider a basketball (which is nearly spherical) and an American football (which is elongated). The basketball represents a circle (a special case of an ellipse with equal axes), while the football represents an ellipse with a higher eccentricity, showing how the shape can vary while still being classified as an ellipse.

Tangents to an Ellipse

3. Definition of a Tangent Line

A tangent line to a curve is a straight line that touches the curve at a single point without crossing it. For an ellipse, the tangent line at a given point on the ellipse represents the direction in which the ellipse is heading at that point.

Illustrative Explanation: Imagine a car driving along a curved road. At any given moment, the direction the car is facing can be represented by a straight line that just touches the curve of the road without crossing it. This line is analogous to the tangent line at that point on the ellipse.

4. Finding the Equation of the Tangent Line

To find the equation of the tangent line to an ellipse at a specific point, we can use the following method. Given a point $(x_0, y_0)$ on the ellipse defined by the equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ , the equation of the tangent line at that point can be derived using implicit differentiation or the point-slope form of a line.

The equation of the tangent line can be expressed as:

$\frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1$

Illustrative Explanation: If you have a point on the ellipse, say 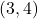$(3, 4)$ , and you want to find the tangent line at that point, you can plug the coordinates into the equation above. This will give you a straight line that just touches the ellipse at 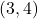$(3, 4)$ without crossing it.

5. Geometric Interpretation of Tangents

Geometrically, the tangent line at a point on the ellipse can be visualized as the line that best approximates the curve at that point. It represents the instantaneous direction of the ellipse at that point.

Illustrative Explanation: Picture a roller coaster at the peak of a hill. The tangent line at the peak represents the direction the roller coaster would travel if it were to continue moving in a straight line at that moment. This is similar to how the tangent line represents the direction of the ellipse at a specific point.

Properties of Tangents to an Ellipse

6. Number of Tangents from a Point

From any external point in relation to an ellipse, there can be two tangents drawn to the ellipse. If the point lies inside the ellipse, no tangents can be drawn, and if the point lies on the ellipse, there is exactly one tangent.

Illustrative Explanation: Imagine standing outside a circular pond. You can throw two sticks that just touch the edge of the pond without falling in. If you were to stand inside the pond, you wouldn’t be able to throw a stick that touches the edge without crossing into the water. This illustrates how the position of a point relative to the ellipse affects the number of tangents.

7. Length of the Tangent Segment

The length of the tangent segment from an external point $(x_1, y_1)$ to the ellipse can be calculated using the formula:

$L = \sqrt{\left(\frac{a^2y_1^2 + b^2x_1^2 - a^2b^2}{b^2}\right)}$

Where $L$ is the length of the tangent segment.

Illustrative Explanation: If you have a point outside the ellipse and you want to know how far the tangent line extends before it touches the ellipse, you can use this formula. It’s like measuring the distance from a point on the ground to the point where a ladder touches a wall (the ellipse) at a tangent.

Applications of Tangents to an Ellipse

8. Engineering and Design

Tangents to ellipses are used in engineering and design, particularly in the design of gears, wheels, and other mechanical components where elliptical shapes are involved. Understanding the tangent lines helps in ensuring that parts fit together smoothly.

Illustrative Explanation: Consider the design of a gear that has an elliptical shape. Engineers must ensure that the teeth of the gear align properly with the tangent lines to ensure smooth operation. If the tangents are not correctly calculated, the gear may not function as intended.

9. Astronomy and Orbits

In astronomy, the orbits of celestial bodies can often be approximated as ellipses. Understanding the tangents to these orbits is crucial for predicting the paths of planets and satellites.

Illustrative Explanation: Imagine a planet orbiting a star in an elliptical path. The tangent lines at various points in the orbit represent the direction in which the planet is moving at that moment. This information is vital for calculating future positions and trajectories.

10. Computer Graphics

In computer graphics, tangents to curves, including ellipses, are essential for rendering smooth curves and animations. Understanding how to calculate tangents allows for more realistic motion and transitions.

Illustrative Explanation: When animating a character moving along a curved path, the tangent lines at various points help determine the direction and speed of the character. This ensures that the movement appears natural and fluid.

Conclusion

In conclusion, tangents to an ellipse are a fundamental concept in mathematics and have significant implications in various fields, including engineering, astronomy, and computer graphics. Understanding the properties of ellipses, the definition and calculation of tangent lines, and their applications provides valuable insights into the behavior of curves and their interactions with straight lines. As we continue to explore the principles of geometry and their applications, the study of tangents to ellipses will remain a key component of our understanding of mathematical shapes and their properties.

Blog.Pengayaan.Com