Triangular numbers are a fascinating sequence of numbers that arise from the arrangement of objects in the shape of an equilateral triangle. They have significant applications in mathematics, combinatorics, and number theory. This article will delve into the definition of triangular numbers, their properties, formulas for calculating them, their visual representation, and their applications, along with illustrative explanations for each concept.
Definition of Triangular Numbers
A triangular number is a number that can be represented as a triangle with dots. The 
-th triangular number is the sum of the first natural numbers. The sequence of triangular numbers starts with 1, 3, 6, 10, 15, and so on. The -th triangular number can be denoted as 
.
Formula for Triangular Numbers
The formula for calculating the -th triangular number is given by:
![\[ T_n = \frac{n(n + 1)}{2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-827e13db71ed31b7cc1e53b234f66a2f_l3.png "Rendered by QuickLaTeX.com")
where is a positive integer representing the position in the sequence.
Illustrative Explanation
To understand this formula, consider the first few triangular numbers:
- For
:
![\[ T_1 = \frac{1(1 + 1)}{2} = \frac{1 \times 2}{2} = 1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d56191f1edecd856ca68e2e241977fd6_l3.png "Rendered by QuickLaTeX.com")
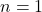This represents a single dot.
- For
:
![\[ T_2 = \frac{2(2 + 1)}{2} = \frac{2 \times 3}{2} = 3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-54a8a82ec175f9812b1985e8c8ad5b6f_l3.png "Rendered by QuickLaTeX.com")
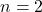This can be visualized as:
“`
•
• •
“`
Here, three dots form a triangle.
- For
:
![\[ T_3 = \frac{3(3 + 1)}{2} = \frac{3 \times 4}{2} = 6 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f2d9c6c880fbe19a2483b4b2ca61f068_l3.png "Rendered by QuickLaTeX.com")
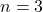This can be visualized as:
“`
•
• •
• • •
“`
Six dots can be arranged to form a triangle.
- For
:
![\[ T_4 = \frac{4(4 + 1)}{2} = \frac{4 \times 5}{2} = 10 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-849ce25b7512dc2306d3c41534fab068_l3.png "Rendered by QuickLaTeX.com")
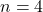This can be visualized as:
“`
•
• •
• • •
• • • •
“`
Ten dots can be arranged to form a larger triangle.
Properties of Triangular Numbers
Triangular numbers possess several interesting properties:
1. Sum of Natural Numbers: Each triangular number is the sum of the first natural numbers. This property can be expressed as:
![\[ T_n = 1 + 2 + 3 + \ldots + n \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-335871a0440df39078ee09728b6a1bfc_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
For example, the 4th triangular number 
can be calculated as:
![\[ T_4 = 1 + 2 + 3 + 4 = 10 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d3adc8eea37984535ace3860bda68ed3_l3.png "Rendered by QuickLaTeX.com")
This reinforces the idea that triangular numbers represent the cumulative sum of natural numbers.
2. Even and Odd Triangular Numbers: Triangular numbers can be either even or odd. The parity of a triangular number depends on the value of :
- If 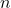is even, 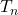is even.
- If 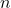is odd, 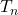is odd.
Illustrative Explanation
- For 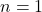(odd),
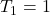(odd). - For 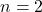(even),
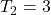(odd). - For 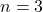(odd),
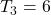(even). - For 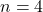(even),
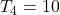(even).
3. Triangular Number Patterns: Triangular numbers exhibit patterns in their differences. The difference between consecutive triangular numbers is equal to the next natural number:
![\[ T_n - T_{n-1} = n \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0c0f6247bde076ed92cb6ef0a03001cc_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
This shows that the difference between each triangular number and the previous one corresponds to the position in the sequence.
4. Triangular Numbers and Polygonal Numbers: Triangular numbers are a specific case of polygonal numbers. They can be represented as the sum of the first integers, while other polygonal numbers represent sums of integers arranged in different shapes (e.g., squares, pentagons).
Visual Representation of Triangular Numbers
Triangular numbers can be visually represented using dots arranged in a triangular formation. This geometric representation helps to understand the concept of triangular numbers intuitively.
Illustrative Explanation
- T1: 1 dot
“`
•
“`
- T2: 3 dots
“`
•
• •
“`
- T3: 6 dots
“`
•
• •
• • •
“`
- T4: 10 dots
“`
•
• •
• • •
• • • •
“`
This visual representation emphasizes how triangular numbers can be formed by stacking rows of dots, where each row corresponds to a natural number.
Applications of Triangular Numbers
Triangular numbers have various applications in mathematics and beyond:
1. Combinatorics: Triangular numbers are used in combinatorial problems, particularly in counting combinations and arrangements. For example, the number of ways to choose 2 objects from objects is given by the triangular number 
.
Illustrative Explanation
If you have 4 objects, the number of ways to choose 2 objects is:
![\[ T_{4-1} = T_3 = 6 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e7a7cad402fb0198916baad2be953f32_l3.png "Rendered by QuickLaTeX.com")
This means there are 6 ways to choose 2 objects from 4.
2. Games and Puzzles: Triangular numbers often appear in games and puzzles, such as arranging objects in triangular formations or solving problems involving triangular patterns.
Illustrative Explanation
In a game where players must arrange tokens in a triangular shape, the number of tokens needed corresponds to triangular numbers. For example, to create a triangle with 5 rows, you would need 
tokens.
3. Mathematical Patterns: Triangular numbers are studied for their mathematical properties and relationships with other number sequences, such as square numbers and pentagonal numbers.
Illustrative Explanation
The relationship between triangular numbers and square numbers can be explored through the formula:
This relationship highlights the interconnectedness of different types of numbers in mathematics.
4. Real-World Applications: Triangular numbers can be found in various real-world contexts, such as arranging seating in a theater, organizing items in a warehouse, or optimizing resources in logistics.
Illustrative Explanation
If a theater has rows of seats arranged in a triangular formation, the total number of seats can be calculated using triangular numbers. For example, if there are 10 rows, the total number of seats would be 
.
Conclusion
In conclusion, triangular numbers are a captivating sequence of numbers that represent the sum of the first natural numbers and can be visually represented in a triangular formation. Their properties, patterns, and applications in combinatorics, games, and real-world scenarios make them an essential topic in mathematics. By understanding triangular numbers, we gain insight into the beauty and interconnectedness of numerical relationships, enhancing our appreciation for the elegance of mathematics. Whether in theoretical exploration or practical application, triangular numbers continue to inspire curiosity and creativity in the world of numbers.