Vector Addition: A Comprehensive Overview

Vector addition is a fundamental concept in physics and mathematics that deals with the combination of vectors to determine a resultant vector. Vectors are quantities that have both magnitude and direction, making them essential for describing various physical phenomena, such as force, velocity, and displacement. Understanding vector addition is crucial for solving problems in mechanics, engineering, and many other fields. In this article, we will explore the definition of vectors, the principles of vector addition, methods for adding vectors, and illustrative examples to provide a thorough understanding of this essential concept.

What is a Vector?

Definition

A vector is a mathematical object that has both magnitude (size) and direction. Vectors are typically represented graphically as arrows, where the length of the arrow indicates the magnitude, and the direction of the arrow indicates the direction of the vector. Common examples of vectors include displacement, velocity, acceleration, and force.

Illustrative Explanation: Imagine a person walking in a park. If they walk 5 meters north, we can represent this movement as a vector. The length of the arrow representing the vector would be proportional to 5 meters, and the arrow would point north to indicate the direction of movement.

Components of a Vector

A vector can be broken down into its components along the coordinate axes. In a two-dimensional Cartesian coordinate system, a vector $\mathbf{A}$ can be expressed in terms of its horizontal (x) and vertical (y) components:

$\mathbf{A} = A_x \hat{i} + A_y \hat{j}$

where:

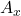$A_x$ is the horizontal component,
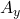$A_y$ is the vertical component,
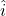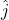$\hat{i}$ and $\hat{j}$ are the unit vectors in the x and y directions, respectively.
Illustrative Explanation: Consider a vector representing a wind blowing at an angle. If the wind has a speed of 10 meters per second at an angle of 30 degrees to the horizontal, we can break this vector into its x and y components. The x-component represents the wind’s speed in the horizontal direction, while the y-component represents the vertical speed.

Principles of Vector Addition

1. Resultant Vector

The resultant vector is the vector that results from the addition of two or more vectors. It represents the combined effect of the individual vectors. The process of finding the resultant vector is known as vector addition.

Illustrative Explanation: Imagine two people pushing a car in different directions. If one person pushes the car to the east with a force of 100 N and another person pushes it to the north with a force of 100 N, the resultant force is the vector sum of these two forces, which will point diagonally northeast.

2. Vector Addition Law

The vector addition law states that the order in which vectors are added does not affect the resultant vector. This property is known as the commutative property of vector addition:

$\mathbf{A} + \mathbf{B} = \mathbf{B} + \mathbf{A}$

Illustrative Explanation: Think of two friends meeting at a café. If one friend arrives first and waits for the other, it doesn’t matter who arrives first; they will still meet at the same location. Similarly, the order of vector addition does not change the resultant vector.

3. Graphical Representation

Vectors can be added graphically using the head-to-tail method or the parallelogram method. These methods provide a visual representation of vector addition.

Illustrative Explanation: Imagine drawing a path on a map. If you walk 3 kilometers east and then 4 kilometers north, you can visualize this by drawing an arrow for each leg of the journey. The head-to-tail method involves placing the tail of the second vector at the head of the first vector, while the parallelogram method involves drawing both vectors from the same starting point to form a parallelogram, with the diagonal representing the resultant vector.

Methods of Vector Addition

1. Head-to-Tail Method

The head-to-tail method involves placing the tail of one vector at the head of another vector. The resultant vector is drawn from the tail of the first vector to the head of the last vector.

Illustrative Explanation: Picture a person walking from point A to point B and then from point B to point C. To find the total displacement from point A to point C, you can draw an arrow from A to B and then another arrow from B to C. The resultant vector is the direct arrow from A to C.

2. Parallelogram Method

The parallelogram method involves drawing two vectors from the same starting point, forming a parallelogram. The diagonal of the parallelogram represents the resultant vector.

Illustrative Explanation: Imagine two forces acting on a box at the same time. If one force pulls the box to the right and another force pulls it upward, you can visualize these forces as two sides of a parallelogram. The diagonal of the parallelogram represents the net force acting on the box.

3. Analytical Method

In the analytical method, vectors are added using their components. The resultant vector’s components are found by summing the corresponding components of the individual vectors.

Illustrative Explanation: Consider a vector representing a car’s velocity of 60 km/h at an angle of 30 degrees. By breaking this vector into its x and y components, you can calculate the total velocity in each direction. The resultant vector can then be found by summing these components.

Example of Analytical Method

Let’s say we have two vectors:

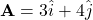$\mathbf{A} = 3 \hat{i} + 4 \hat{j}$ (3 units in the x-direction and 4 units in the y-direction)
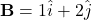$\mathbf{B} = 1 \hat{i} + 2 \hat{j}$ (1 unit in the x-direction and 2 units in the y-direction)

To find the resultant vector $\mathbf{R}$ :

$\mathbf{R} = \mathbf{A} + \mathbf{B} = (3 + 1) \hat{i} + (4 + 2) \hat{j} = 4 \hat{i} + 6 \hat{j}$

The resultant vector $\mathbf{R}$ has components of 4 in the x-direction and 6 in the y-direction.

Applications of Vector Addition

Vector addition is widely used in various fields, including physics, engineering, navigation, and computer graphics. Here are some key applications:

1. Physics

In physics, vector addition is essential for analyzing forces, velocities, and accelerations. It helps in solving problems related to motion, equilibrium, and dynamics.

Illustrative Explanation: Consider a scenario where multiple forces act on an object, such as a box being pushed by two people in different directions. By using vector addition, you can determine the net force acting on the box and predict its motion.

2. Engineering

Engineers use vector addition to analyze forces in structures, such as bridges and buildings. Understanding how forces combine helps ensure the safety and stability of structures.

Illustrative Explanation: Imagine an engineer designing a bridge. By analyzing the forces acting on the bridge (such as weight, wind, and tension), the engineer can use vector addition to ensure that the bridge can withstand these forces without collapsing.

3. Navigation

In navigation, vector addition is used to determine the resultant path of a vehicle or aircraft. By considering wind speed and direction, navigators can calculate the actual course needed to reach a destination.

Illustrative Explanation: Think of a pilot flying an airplane. If the plane is heading north but there is a strong wind blowing from the west, the pilot must account for this wind vector to maintain the intended flight path. By using vector addition, the pilot can adjust the heading to reach the destination accurately.

4. Computer Graphics

In computer graphics, vector addition is used to manipulate objects in a virtual environment. By adding vectors, graphics programmers can create realistic movements and animations.

Illustrative Explanation: Imagine a video game character moving in a 3D environment. The character’s movement can be represented as vectors. By adding these vectors, the game engine can calculate the character’s new position and orientation in the virtual world.

Conclusion

Vector addition is a fundamental concept that plays a crucial role in various scientific and engineering disciplines. By understanding the principles of vector addition, including the methods for adding vectors and the applications of this concept, we can analyze and solve problems related to forces, motion, and other physical phenomena. Through illustrative examples and explanations, we can appreciate the significance of vector addition in our understanding of the physical world. Whether in physics, engineering, navigation, or computer graphics, vector addition serves as a vital tool that enhances our ability to model and predict the behavior of complex systems. As we continue to explore the intricacies of vectors and their interactions, the principles of vector addition will remain essential for our understanding and application of science and technology.

Blog.Pengayaan.Com