Velocity is a fundamental concept in physics that describes the rate of change of an object’s position with respect to time. Unlike speed, which is a scalar quantity that only considers how fast an object is moving, velocity is a vector quantity that includes both magnitude and direction. This distinction makes velocity a crucial concept for understanding motion in a more comprehensive way. In this extensive exploration of velocity, we will delve into its definition, mathematical formulation, types, relationship with other physical quantities, applications, and significance in various fields.
Definition of Velocity
Velocity is defined as the displacement of an object per unit of time. Displacement refers to the change in position of an object, taking into account both the distance traveled and the direction of that travel. The basic formula for calculating velocity (![]() ) is given by:
) is given by:
![]()
Where:
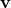 is the velocity vector (in meters per second, m/s).
is the velocity vector (in meters per second, m/s).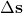 is the displacement vector (in meters, m).
is the displacement vector (in meters, m).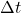 is the time interval during which the displacement occurs (in seconds, s).
is the time interval during which the displacement occurs (in seconds, s).
This formula indicates that velocity is the rate at which an object changes its position, incorporating both the distance and the direction of that change.
Mathematical Formulation
Velocity can be expressed in various contexts, and its mathematical formulation can vary depending on the nature of the motion. Here are some key formulations:
1. Average Velocity: The average velocity of an object over a given time interval can be calculated using the total displacement divided by the total time taken:
![]()
This formula is useful for determining the overall velocity of an object when it travels different distances in different directions.
2. Instantaneous Velocity: The instantaneous velocity of an object is the velocity at a specific moment in time. It can be determined by taking the derivative of the position with respect to time:
![]()
Where ![]() is an infinitesimally small change in position. This concept is particularly important in calculus and physics when analyzing motion.
is an infinitesimally small change in position. This concept is particularly important in calculus and physics when analyzing motion.
3. Velocity in Different Dimensions: In two or three dimensions, velocity can be expressed in terms of its components. For example, if an object moves in a plane with coordinates ![]() , the velocity can be calculated using the components of velocity in the x and y directions:
, the velocity can be calculated using the components of velocity in the x and y directions:
![]()
Where ![]() and
and ![]() are the components of velocity in the x and y directions, respectively, and
are the components of velocity in the x and y directions, respectively, and ![]() and
and ![]() are the unit vectors in those directions.
are the unit vectors in those directions.
Types of Velocity
Velocity can be categorized into several types based on the context of motion:
- Constant Velocity: An object is said to be moving at a constant velocity if it covers equal displacements in equal intervals of time, regardless of the duration of the time intervals. For example, a car traveling in a straight line at a steady speed of 60 km/h is moving at a constant velocity.
- Variable Velocity: An object experiences variable velocity when it covers different displacements in equal time intervals. For instance, a car accelerating from a stoplight to a higher speed is an example of variable velocity.
- Average Velocity: Average velocity is calculated over a specific displacement and time period. It provides a general idea of how fast an object has traveled over that interval, taking into account the direction of travel.
- Instantaneous Velocity: Instantaneous velocity refers to the velocity of an object at a specific moment in time. It is often measured using speedometers in vehicles or through radar guns in law enforcement.
Relationship with Other Physical Quantities
Velocity is closely related to several other physical quantities, including:
1. Speed: While speed is a scalar quantity that measures how fast an object is moving, velocity is a vector quantity that includes both magnitude and direction. The relationship between speed and velocity can be expressed as:
![]()
Where ![]() is the speed (magnitude of velocity). In cases where the motion is in a straight line and the direction is constant, speed and velocity can be used interchangeably.
is the speed (magnitude of velocity). In cases where the motion is in a straight line and the direction is constant, speed and velocity can be used interchangeably.
2. Acceleration: Acceleration is the rate of change of velocity with respect to time. It can be calculated as:
![]()
Where ![]() is acceleration,
is acceleration, ![]() is the change in velocity, and
is the change in velocity, and ![]() is the change in time. Acceleration can occur due to changes in speed, direction, or both.
is the change in time. Acceleration can occur due to changes in speed, direction, or both.
3. Displacement: Displacement is the vector quantity that represents the change in position of an object. Velocity is directly related to displacement, as it is defined as the rate of change of displacement with respect to time.
Applications of Velocity
Velocity has a wide range of applications across various fields, including:
- Transportation: In transportation, velocity is a critical factor in determining travel times, fuel efficiency, and safety. Understanding velocity limits and vehicle performance is essential for road safety and traffic management.
- Sports: In sports, velocity is a key performance metric. Athletes often train to improve their velocity in various disciplines, such as running, swimming, and cycling. Coaches analyze velocity to optimize training regimens and strategies.
- Engineering: In engineering, velocity is crucial for designing machines, vehicles, and systems. Engineers must consider velocity when developing components such as gears, motors, and turbines to ensure optimal performance.
- Physics and Research: In scientific research, velocity is a fundamental parameter in experiments and studies involving motion. Physicists analyze velocity to understand the behavior of particles, waves, and other phenomena.
- Meteorology: In meteorology, wind velocity is an important factor in weather forecasting and climate studies. Understanding wind velocity helps predict weather patterns, storm behavior, and environmental changes.
Factors Influencing Velocity
Several factors can influence the velocity of an object:
1. Mass: The mass of an object can affect its velocity, particularly when considering forces acting on it. According to Newton’s second law, the acceleration of an object is inversely proportional to its mass when a constant force is applied:
![]()
This means that a heavier object will accelerate more slowly than a lighter object under the same force, affecting its velocity.
2. Friction: Friction is a force that opposes motion and can significantly affect velocity. The type and amount of friction between surfaces can either hinder or facilitate movement, impacting the overall velocity of an object.
3. Incline: The angle of an incline can influence the velocity of an object moving down or up a slope. Objects tend to accelerate faster down a steeper incline due to the increased component of gravitational force acting along the slope.
4. Air Resistance: For objects moving through the air, air resistance (drag) can affect velocity. As velocity increases, the force of air resistance also increases, which can limit the maximum velocity an object can achieve.
Conclusion
In conclusion, velocity is a fundamental concept in physics that describes the rate of change of an object’s position with respect to time, incorporating both magnitude and direction. Its definition, mathematical formulation, types, relationship with other physical quantities, applications, and influencing factors provide a comprehensive understanding of motion. From transportation and sports to engineering and scientific research, velocity plays a critical role in shaping our understanding of the physical world. As research and technology continue to evolve, the study of velocity will remain a vital area of exploration, driving advancements in science, engineering, and everyday life. Understanding velocity not only enhances our knowledge of motion but also informs practical applications that impact our daily lives and the development of new technologies.