The wave function is a fundamental concept in quantum mechanics that describes the quantum state of a particle or system of particles. It encapsulates all the information about a quantum system and is central to understanding phenomena at the microscopic scale. This article will delve into the definition of the wave function, its mathematical representation, physical interpretation, properties, applications, and significance in quantum mechanics, providing illustrative explanations for each concept.
Definition of Wave Function
In quantum mechanics, the wave function is a mathematical function that describes the probability amplitude of a particle’s position and momentum. It is typically denoted by the Greek letter psi (![]() ) and is a complex-valued function of position and time. The square of the absolute value of the wave function,
) and is a complex-valued function of position and time. The square of the absolute value of the wave function, ![]() , gives the probability density of finding a particle at a particular position
, gives the probability density of finding a particle at a particular position ![]() at time
at time ![]() .
.
Illustrative Explanation
Imagine a wave traveling through water. Just as the height of the water wave at any point can tell you how high the water is at that location, the wave function tells you about the likelihood of finding a particle in a specific location. If you visualize the wave function as a surface above a graph, the peaks represent areas where the particle is more likely to be found, while the troughs represent areas where it is less likely to be found.
Mathematical Representation of the Wave Function
The wave function can be expressed mathematically as:
![]()
Where:
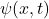 is the wave function as a function of position
is the wave function as a function of position 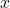 and time
and time 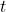 .
. is the amplitude of the wave function.
is the amplitude of the wave function.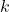 is the wave number, related to the wavelength of the wave.
is the wave number, related to the wavelength of the wave.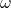 is the angular frequency, related to the energy of the wave.
is the angular frequency, related to the energy of the wave.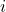 is the imaginary unit.
is the imaginary unit.
Illustrative Explanation
Consider a simple wave traveling along a string. The wave function describes how the displacement of the string varies with position and time. The amplitude ![]() represents the maximum displacement from the equilibrium position, while the wave number
represents the maximum displacement from the equilibrium position, while the wave number ![]() tells you how many wavelengths fit into a given distance. The angular frequency
tells you how many wavelengths fit into a given distance. The angular frequency ![]() indicates how quickly the wave oscillates over time.
indicates how quickly the wave oscillates over time.
Physical Interpretation of the Wave Function
The wave function has a probabilistic interpretation, which is one of the key departures from classical physics. The square of the absolute value of the wave function, ![]() , represents the probability density of finding a particle at position
, represents the probability density of finding a particle at position ![]() at time
at time ![]() . This means that if you were to measure the position of the particle, the likelihood of finding it in a small interval around
. This means that if you were to measure the position of the particle, the likelihood of finding it in a small interval around ![]() is proportional to
is proportional to ![]() .
.
Illustrative Explanation
Imagine you have a dartboard, and you throw darts at it. If you throw many darts, some areas of the board will have more darts clustered together, while others will have fewer. The wave function acts like a map of where the darts (representing the particle’s position) are likely to land. Areas with a higher probability density (higher ![]() ) correspond to regions where you would expect to find more darts.
) correspond to regions where you would expect to find more darts.
Properties of the Wave Function
The wave function has several important properties:
1. Normalization: The total probability of finding a particle in all space must equal one. This requirement leads to the normalization condition:
![]()
This ensures that the wave function is properly scaled to represent a valid probability distribution.
Illustrative Explanation
Think of a pie chart representing the distribution of a quantity. If the pie chart is not complete (i.e., the total area does not equal one), it cannot accurately represent the distribution. Similarly, the normalization condition ensures that the wave function accurately describes the probability of finding a particle.
2. Superposition: The wave function can exist in a superposition of states, meaning that a quantum system can be in multiple states simultaneously. If ![]() and
and ![]() are two valid wave functions, then their linear combination
are two valid wave functions, then their linear combination ![]() is also a valid wave function.
is also a valid wave function.
Illustrative Explanation
Imagine a musical chord made up of different notes. Each note represents a different wave function, and when played together, they create a harmonious sound. Similarly, the superposition principle allows multiple wave functions to combine, resulting in a new wave function that describes the system.
3. Complex Nature: The wave function is generally a complex function, meaning it has both real and imaginary parts. This complexity is essential for capturing the full behavior of quantum systems, including interference and phase relationships.
Illustrative Explanation
Consider a rotating vector in a plane. The vector can be described using its length (magnitude) and direction (angle). The real part of the wave function can be thought of as the horizontal component of this vector, while the imaginary part represents the vertical component. Together, they provide a complete description of the wave function’s behavior.
Applications of the Wave Function
The wave function is central to many areas of physics and has numerous applications:
1. Quantum Mechanics: The wave function is the cornerstone of quantum mechanics, providing a complete description of quantum systems. It is used to calculate probabilities, energy levels, and transition rates in quantum systems.
Illustrative Explanation
In quantum mechanics, the wave function allows physicists to predict the behavior of particles, such as electrons in an atom. By solving the Schrödinger equation, which describes how the wave function evolves over time, scientists can determine the allowed energy levels of electrons and their spatial distributions.
2. Quantum Chemistry: In quantum chemistry, the wave function is used to describe the electronic structure of atoms and molecules. It helps chemists understand chemical bonding, reaction mechanisms, and molecular properties.
Illustrative Explanation
When studying a molecule, chemists use the wave function to determine how electrons are distributed around the nuclei. This information is crucial for predicting how the molecule will react with other substances and what properties it will exhibit.
3. Quantum Computing: The wave function plays a vital role in quantum computing, where quantum bits (qubits) can exist in superpositions of states. This property allows quantum computers to perform complex calculations much faster than classical computers.
Illustrative Explanation
Imagine a light switch that can be both on and off at the same time. In quantum computing, qubits can represent multiple states simultaneously, enabling parallel processing and more efficient algorithms. The wave function describes the state of these qubits and their interactions.
Significance of the Wave Function
The wave function is significant in understanding the fundamental principles of quantum mechanics and the behavior of matter at the microscopic scale. It provides a framework for describing and predicting the outcomes of quantum experiments, leading to profound insights into the nature of reality.
Illustrative Explanation
Think of the wave function as a map of a hidden landscape. While we cannot see the landscape directly, the wave function provides us with the tools to navigate it. By understanding the wave function, we can make predictions about where particles are likely to be found, how they will interact, and what phenomena will emerge from their behavior.
Conclusion
In conclusion, the wave function is a fundamental concept in quantum mechanics characterized by its role in describing the quantum state of particles and systems. Understanding the mathematical representation, physical interpretation, properties, applications, and significance of the wave function is essential for grasping various physical phenomena. From quantum mechanics to quantum chemistry and quantum computing, the wave function plays a vital role in our understanding of the microscopic world. By appreciating the intricacies of the wave function, we can better navigate its implications in both scientific and practical contexts.