Dalam fisika, konsep massa merupakan salah satu besaran paling mendasar yang digunakan untuk mendeskripsikan sifat suatu benda. Massa bukan hanya sekadar angka pada timbangan, tetapi juga memiliki peran besar dalam berbagai hukum fisika, seperti Hukum Newton, Hukum Kekekalan Energi, dan Prinsip Gravitasi. Untuk memastikan konsistensi dalam pengukuran dan perhitungan ilmiah, digunakan dimensi massa, yang berfungsi sebagai dasar dalam analisis dimensi serta memastikan kesesuaian dalam berbagai persamaan fisika.
Artikel ini akan membahas konsep dimensi massa, bagaimana massa diukur, serta pentingnya memahami dimensi ini dalam kehidupan sehari-hari dan ilmu pengetahuan.
Apa Itu Dimensi Massa?
Dimensi dalam fisika adalah cara untuk menyatakan sifat fundamental dari suatu besaran dalam bentuk kombinasi dari besaran dasar. Massa, sebagai salah satu besaran pokok dalam Sistem Internasional (SI), memiliki dimensi dasar yang dinyatakan dengan
![]()
.
Dalam sistem SI, massa diukur dalam satuan kilogram (kg) dan digunakan sebagai dasar untuk banyak perhitungan ilmiah lainnya, termasuk gaya, energi, dan momentum.
Ilustrasi Konsep:
Bayangkan Anda ingin menentukan hubungan antara massa, percepatan, dan gaya dalam Hukum Kedua Newton:
![]()
Dimensi dari masing-masing besaran adalah:
- Gaya (
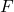 ):
): ![Rendered by QuickLaTeX.com [M][L][T]^{-2}](https://pengayaan.com/wp-content/uploads/2025/02/3_Dimensi-Massa.png)
- Massa (
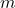 ):
): ![Rendered by QuickLaTeX.com [M]](https://pengayaan.com/wp-content/uploads/2025/02/5_Dimensi-Massa.png)
- Percepatan (
 ):
): ![Rendered by QuickLaTeX.com [L][T]^{-2}](https://pengayaan.com/wp-content/uploads/2025/02/7_Dimensi-Massa.png)
Karena dimensi harus sesuai dalam suatu persamaan, maka kita bisa melihat bagaimana massa berperan dalam menentukan dimensi dari gaya.
Mengapa Dimensi Massa Penting?
Dimensi massa sangat penting karena membantu dalam berbagai aspek pengukuran dan perhitungan ilmiah. Beberapa alasan utama mengapa kita harus memahami konsep ini meliputi:
1. Konsistensi dalam Perhitungan Fisika
Dimensi massa memungkinkan ilmuwan dan insinyur untuk memverifikasi persamaan fisika dan memastikan kesesuaian antara besaran yang digunakan.
Ilustrasi:
Jika kita ingin menghitung energi kinetik suatu benda, rumusnya adalah:
![]()
Dimensi dari setiap komponen adalah:
- Energi (
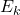 ):
): ![Rendered by QuickLaTeX.com [M][L]^2[T]^{-2}](https://pengayaan.com/wp-content/uploads/2025/02/10_Dimensi-Massa.png)
- Massa (
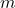 ):
): ![Rendered by QuickLaTeX.com [M]](https://pengayaan.com/wp-content/uploads/2025/02/5_Dimensi-Massa.png)
- Kecepatan (
 ):
): ![Rendered by QuickLaTeX.com [L][T]^{-1}](https://pengayaan.com/wp-content/uploads/2025/02/12_Dimensi-Massa.png)
Setelah substitusi, hasil akhirnya menunjukkan bahwa dimensi energi memang sesuai dengan persamaan, membuktikan bahwa perhitungan tersebut benar.
2. Memastikan Kesatuan dalam Pengukuran
Dalam berbagai bidang, terutama sains dan teknik, penting untuk memiliki satuan yang seragam agar tidak terjadi kesalahan dalam pengukuran.
Ilustrasi:
Jika seorang insinyur di Eropa menggunakan satuan kilogram (kg) tetapi seorang ilmuwan di Amerika Serikat menggunakan pound (lb) tanpa melakukan konversi yang benar, maka kesalahan dalam desain dan perhitungan bisa terjadi, yang dapat menyebabkan kegagalan dalam proyek teknik atau eksperimen ilmiah.
3. Membedakan Massa dan Berat
Banyak orang sering menganggap bahwa massa dan berat adalah hal yang sama, padahal keduanya berbeda. Massa adalah jumlah materi dalam suatu benda, sedangkan berat adalah gaya gravitasi yang bekerja pada benda tersebut.
Ilustrasi:
Jika seseorang memiliki massa 70 kg di Bumi, maka beratnya bisa dihitung dengan:
![]()
Dengan ![]() , maka:
, maka:
![]()
Namun, jika orang yang sama berada di Bulan dengan gravitasi hanya 1/6 dari Bumi, beratnya akan lebih kecil, tetapi massanya tetap 70 kg.
4. Aplikasi dalam Hukum Kekekalan Massa
Hukum Kekekalan Massa menyatakan bahwa dalam sistem tertutup, massa total akan tetap konstan meskipun terjadi perubahan bentuk atau reaksi kimia.
Ilustrasi:
Dalam pembakaran bensin di mesin mobil, massa total dari bahan bakar dan oksigen yang masuk ke mesin sama dengan massa gas buang dan energi yang dihasilkan. Meskipun bentuk dan wujudnya berubah, massa tetap terjaga.
5. Aplikasi dalam Industri dan Teknologi
Dalam industri, terutama yang berhubungan dengan material dan manufaktur, memahami dimensi massa sangat penting untuk memastikan produk dibuat dengan spesifikasi yang tepat.
Ilustrasi:
Dalam pembuatan pesawat terbang, insinyur harus memastikan bahwa massa komponen pesawat dibagi secara merata untuk menjaga keseimbangan dan kestabilan saat terbang. Jika massa tidak dihitung dengan benar, pesawat bisa kehilangan keseimbangan dan menyebabkan kecelakaan.
Bagaimana Massa Diukur dalam Berbagai Skala?
Massa dapat diukur dalam berbagai skala tergantung pada konteks dan aplikasi.
1. Massa dalam Skala Mikroskopis
Pada tingkat atom dan molekul, massa diukur dalam satuan massa atom (amu) atau dalam kilogram yang sangat kecil.
Ilustrasi:
Sebuah atom karbon memiliki massa sekitar 12 amu, yang setara dengan 1,99 × 10^{-26} kg.
2. Massa dalam Skala Makroskopis
Dalam kehidupan sehari-hari, kita mengukur massa dalam gram, kilogram, atau ton.
Ilustrasi:
- Massa apel sekitar 200 gram.
- Sebuah mobil memiliki massa sekitar 1.500 kg.
3. Massa dalam Skala Astronomis
Dalam dunia astronomi, massa sering diukur dalam massa matahari (![]() ) atau kilogram dalam skala sangat besar.
) atau kilogram dalam skala sangat besar.
Ilustrasi:
Matahari memiliki massa sekitar 1,989 × 10^{30} kg, atau sekitar 330.000 kali massa Bumi.
Kesimpulan
Dimensi massa adalah konsep fundamental dalam fisika yang memastikan konsistensi dalam pengukuran dan perhitungan ilmiah. Massa tidak hanya sekadar angka pada timbangan, tetapi memiliki peran besar dalam berbagai aspek ilmu pengetahuan, industri, dan teknologi.
Pemahaman yang benar tentang dimensi massa membantu kita dalam:
- Memastikan keakuratan dalam perhitungan fisika.
- Menghindari kesalahan dalam konversi satuan dan pengukuran.
- Membedakan antara massa dan berat.
- Memahami hukum kekekalan massa dalam reaksi kimia dan fisika.
- Menerapkan konsep ini dalam industri, teknologi, dan astronomi.
Dengan memahami konsep ini, kita dapat lebih memahami bagaimana alam semesta bekerja dan bagaimana teknologi di sekitar kita dirancang untuk berfungsi dengan efisien dan aman.
