Kelajuan rata-rata adalah konsep penting dalam fisika yang sering digunakan untuk memahami gerak benda dalam kehidupan sehari-hari. Dalam konteks sederhana, kelajuan rata-rata mengukur seberapa jauh suatu benda bergerak dalam satu satuan waktu, tanpa memperhatikan perubahan kecepatan selama perjalanan. Konsep ini bermanfaat untuk menganalisis gerak benda seperti kendaraan di jalan, aktivitas olahraga, atau bahkan aliran air dalam pipa.
Artikel ini akan menjelaskan apa itu kelajuan rata-rata, bagaimana menghitungnya, serta aplikasinya dalam kehidupan sehari-hari dengan ilustrasi yang relevan.
Apa Itu Kelajuan Rata-Rata?
Kelajuan rata-rata adalah total jarak yang ditempuh oleh suatu benda dibagi dengan total waktu yang diperlukan untuk menempuh jarak tersebut. Dalam persamaan matematis, kelajuan rata-rata dirumuskan sebagai:
![\[ v_{\text{rata-rata}} = \frac{s}{t} \]](https://pengayaan.com/wp-content/uploads/2024/11/Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
di mana:
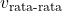adalah kelajuan rata-rata (m/s atau km/jam),
adalah total jarak yang ditempuh (m atau km), dan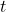
adalah total waktu yang digunakan (s atau jam).
Kelajuan rata-rata tidak mempertimbangkan percepatan atau perlambatan selama perjalanan, melainkan hanya fokus pada hubungan antara total jarak dan waktu.
1. Kelajuan Rata-Rata Kendaraan di Jalan
Salah satu aplikasi paling umum dari kelajuan rata-rata adalah saat menganalisis perjalanan kendaraan di jalan. Saat mengemudi, kita mungkin menghadapi situasi di mana kendaraan bergerak dengan kecepatan yang bervariasi karena kondisi lalu lintas, jalan menanjak, atau lampu merah. Namun, kelajuan rata-rata membantu kita mengetahui efisiensi perjalanan secara keseluruhan.
Ilustrasi:
Misalkan Anda melakukan perjalanan sejauh 120 km. Dalam separuh perjalanan pertama (60 km), Anda bergerak dengan kecepatan 80 km/jam, dan dalam separuh berikutnya (60 km), kecepatan Anda menurun menjadi 40 km/jam karena lalu lintas padat. Total waktu perjalanan adalah:
- Waktu untuk 60 km pertama:
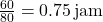, - Waktu untuk 60 km kedua:
.
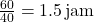Total waktu perjalanan: 
.
Kelajuan rata-rata perjalanan adalah:
![\[ v_{\text{rata-rata}} = \frac{s}{t} = \frac{120}{2.25} \approx 53.3 \, \text{km/jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/7_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
2. Pelari Maraton
Dalam dunia olahraga, kelajuan rata-rata sering digunakan untuk mengukur kinerja atlet, khususnya pelari maraton. Seorang pelari mungkin memulai dengan kecepatan tinggi tetapi melambat di tengah lomba karena kelelahan. Dengan menghitung kelajuan rata-rata, kita dapat mengevaluasi seberapa cepat pelari tersebut menyelesaikan seluruh jarak.
Ilustrasi:
Seorang pelari menyelesaikan maraton sejauh 42 km dalam waktu 3 jam. Kelajuan rata-rata pelari dapat dihitung sebagai:
![\[ v_{\text{rata-rata}} = \frac{s}{t} = \frac{42}{3} = 14 \, \text{km/jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/8_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
Meskipun kecepatan pelari mungkin bervariasi selama lomba, kelajuan rata-rata menunjukkan kinerja keseluruhan.
3. Penerbangan Pesawat
Saat bepergian dengan pesawat, kelajuan rata-rata digunakan untuk memperkirakan waktu tempuh perjalanan. Pesawat sering mengalami perubahan kecepatan karena angin atau kondisi atmosfer, tetapi kelajuan rata-rata memberikan gambaran yang berguna tentang waktu perjalanan.
Ilustrasi:
Misalkan sebuah pesawat menempuh perjalanan sejauh 1.500 km. Selama 1 jam pertama, pesawat bergerak dengan kecepatan 600 km/jam, tetapi pada jam berikutnya, kecepatan menurun menjadi 400 km/jam karena menghadapi angin. Total waktu perjalanan adalah:
![\[ t = \frac{1.500}{v_{\text{rata-rata}}}. \]](https://pengayaan.com/wp-content/uploads/2024/11/9_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
Dengan kecepatan rata-rata:
![\[ v_{\text{rata-rata}} = \frac{600 \times 1 + 400 \times 1}{2} = 500 \, \text{km/jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/10_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
Waktu perjalanan:
![\[ t = \frac{1.500}{500} = 3 \, \text{jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/11_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
4. Pengiriman Barang
Dalam logistik dan pengiriman barang, kelajuan rata-rata digunakan untuk memastikan barang sampai tepat waktu. Layanan pengiriman menggunakan data ini untuk memperkirakan durasi pengiriman berdasarkan jarak antara lokasi pengambilan dan tujuan.
Ilustrasi:
Misalkan sebuah truk pengiriman membawa barang sejauh 300 km. Karena kondisi jalan, kecepatan truk bervariasi: 60 km/jam selama 2 jam pertama dan 40 km/jam selama 3 jam berikutnya. Total waktu adalah:
![\[ t = 2 + 3 = 5 \, \text{jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/12_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
Kelajuan rata-rata perjalanan adalah:
![\[ v_{\text{rata-rata}} = \frac{s}{t} = \frac{300}{5} = 60 \, \text{km/jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/13_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
5. Perjalanan Bersepeda
Bagi para pesepeda, kelajuan rata-rata menjadi indikator penting untuk melacak kinerja mereka selama latihan atau balapan. Pesepeda sering menghadapi variasi medan seperti tanjakan dan turunan yang memengaruhi kecepatan mereka.
Ilustrasi:
Seorang pesepeda menempuh jarak 50 km. Ia melaju dengan kecepatan 25 km/jam selama 2 jam pertama, kemudian melambat menjadi 10 km/jam selama 1 jam berikutnya. Total waktu perjalanan:
![\[ t = 2 + 1 = 3 \, \text{jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/14_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
Kelajuan rata-rata:
![\[ v_{\text{rata-rata}} = \frac{s}{t} = \frac{50}{3} \approx 16.67 \, \text{km/jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/15_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
6. Arus Air di Pipa
Kelajuan rata-rata tidak hanya digunakan untuk benda bergerak, tetapi juga untuk aliran cairan dalam pipa. Insinyur sering menggunakan konsep ini untuk memastikan distribusi air atau bahan cair lainnya berjalan efisien.
Ilustrasi:
Misalkan air mengalir melalui pipa sepanjang 20 meter dalam waktu 5 detik. Kelajuan rata-rata aliran air adalah:
![\[ v_{\text{rata-rata}} = \frac{s}{t} = \frac{20}{5} = 4 \, \text{m/s}. \]](https://pengayaan.com/wp-content/uploads/2024/11/16_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
7. Transportasi Umum
Kelajuan rata-rata juga menjadi indikator penting untuk mengevaluasi efisiensi transportasi umum, seperti bus atau kereta. Ini membantu operator dalam merencanakan jadwal perjalanan dan memperkirakan waktu tiba.
Ilustrasi:
Sebuah bus menempuh perjalanan sejauh 100 km. Selama perjalanan, bus berhenti di beberapa titik, menyebabkan total waktu tempuh menjadi 3 jam. Kelajuan rata-rata bus adalah:
![\[ v_{\text{rata-rata}} = \frac{s}{t} = \frac{100}{3} \approx 33.33 \, \text{km/jam}. \]](https://pengayaan.com/wp-content/uploads/2024/11/17_Kelajuan-Rata-Rata-dalam-Kehidupan-Sehari-Hari.png "Rendered by QuickLaTeX.com")
Kesimpulan
Kelajuan rata-rata adalah konsep yang sederhana tetapi sangat relevan dalam berbagai aspek kehidupan sehari-hari. Dari perjalanan kendaraan, olahraga, penerbangan, hingga aliran air, kelajuan rata-rata memberikan cara untuk memahami efisiensi gerak dalam berbagai konteks. Dengan memahami konsep ini, kita dapat lebih baik dalam merencanakan waktu, menganalisis performa, dan mengevaluasi efisiensi sistem.
Kelajuan rata-rata membantu kita melihat gambaran keseluruhan gerak, bahkan ketika kecepatan sebenarnya bervariasi sepanjang perjalanan.