Perbedaan Mekanika Lagrangian dan Hamiltonian

Fisika

Dalam fisika klasik, terdapat dua pendekatan utama untuk mempelajari dinamika sistem mekanik, yaitu mekanika Lagrangian dan mekanika Hamiltonian. Kedua pendekatan ini merupakan formulasi yang lebih maju dibandingkan dengan mekanika Newtonian, karena menggunakan konsep energi untuk mendeskripsikan gerakan sistem fisik.

Secara umum, mekanika Lagrangian berfokus pada perbedaan antara energi kinetik dan energi potensial suatu sistem, sedangkan mekanika Hamiltonian menggunakan konsep fungsi energi total sistem dalam bentuk koordinat kanonik dan momentum. Meskipun keduanya dapat menghasilkan hasil yang sama dalam memprediksi pergerakan suatu sistem, mekanika Hamiltonian memiliki keunggulan dalam bidang fisika teoretis, seperti mekanika kuantum dan relativitas umum.

Artikel ini akan membahas secara mendalam perbedaan antara mekanika Lagrangian dan Hamiltonian, bagaimana mereka digunakan, serta keunggulan masing-masing pendekatan dalam berbagai bidang fisika.

Konsep Dasar Mekanika Lagrangian

1. Definisi dan Prinsip Dasar

Mekanika Lagrangian didasarkan pada prinsip Hamilton (Prinsip Tindakan Minimum), yang menyatakan bahwa lintasan nyata suatu sistem mekanik adalah lintasan yang meminimalkan suatu besaran yang disebut aksi.

Dalam mekanika ini, kita mendefinisikan fungsi Lagrangian (L) sebagai:

    \[ L = T - V \]

di mana:

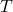  • T = energi kinetik sistem
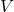  • V = energi potensial sistem

Gerak suatu sistem kemudian ditentukan dengan menyelesaikan persamaan Euler-Lagrange:

    \[ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \right) - \frac{\partial L}{\partial q} = 0 \]

di mana:

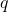  • q adalah koordinat umum sistem
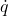  • \dot{q} adalah kecepatan umum (turunan waktu dari q)

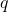Ilustrasi Sederhana

Bayangkan seorang peselancar yang meluncur di atas ombak. Jalur yang diambil oleh peselancar ini tidak sembarangan, tetapi mengikuti lintasan yang meminimalkan usaha dan hambatan. Mekanika Lagrangian mencari lintasan gerak seperti peselancar ini, di mana aksi totalnya adalah minimum.

2. Keunggulan Mekanika Lagrangian

  • Tidak bergantung pada sistem koordinat: Mekanika Lagrangian lebih fleksibel dibandingkan mekanika Newtonian karena dapat digunakan dalam koordinat umum, tidak hanya koordinat kartesian.
  • Cocok untuk sistem dengan banyak partikel: Memudahkan analisis sistem dengan banyak derajat kebebasan.
  • Lebih alami dalam fisika medan: Banyak digunakan dalam relativitas dan teori medan kuantum.

3. Contoh Penerapan Mekanika Lagrangian

  • Gerak planet dalam tata surya: Menentukan lintasan orbit dengan mempertimbangkan pengaruh gravitasi.
  • Pendulum sederhana dan pendulum ganda: Menganalisis sistem osilasi non-linier.
  • Partikel dalam medan elektromagnetik: Digunakan dalam elektrodinamika klasik.

—

Konsep Dasar Mekanika Hamiltonian

1. Definisi dan Prinsip Dasar

Mekanika Hamiltonian adalah formulasi lain dari mekanika klasik yang berfokus pada energi total sistem dalam bentuk koordinat kanonik dan momentum kanonik.

Dalam mekanika ini, kita mendefinisikan fungsi Hamiltonian (H) sebagai:

    \[ H = T + V \]

atau secara umum dalam transformasi Legendre dari Lagrangian:

    \[ H = \sum p_i \dot{q}_i - L \]

di mana:

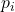  • p_i adalah momentum kanonik yang didefinisikan sebagai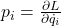 p_i = \frac{\partial L}{\partial \dot{q}_i}
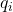  • q_i adalah koordinat umum

Gerak suatu sistem dalam mekanika Hamiltonian ditentukan dengan menyelesaikan persamaan Hamilton:

    \[ \dot{q_i} = \frac{\partial H}{\partial p_i}, \quad \dot{p_i} = -\frac{\partial H}{\partial q_i} \]

Ilustrasi Sederhana

Bayangkan seorang pemain biliar yang mengamati bola biliar tidak hanya berdasarkan posisinya tetapi juga momentumnya. Mekanika Hamiltonian memungkinkan kita untuk memahami gerak sistem dengan meninjau bagaimana energi total sistem berubah seiring waktu dalam ruang fase yang mencakup posisi dan momentum.

2. Keunggulan Mekanika Hamiltonian

  • Lebih cocok untuk sistem dengan banyak derajat kebebasan: Pendekatan ini digunakan dalam fisika statistik dan mekanika kuantum.
  • Dapat digunakan dalam transformasi fase: Memungkinkan pemetaan sistem mekanik dalam ruang fase, yang sangat berguna dalam analisis sistem dinamis dan kekacauan.
  • Lebih mudah digunakan dalam teori kuantum: Mekanika kuantum dibangun berdasarkan prinsip mekanika Hamiltonian, di mana fungsi Hamiltonian berperan sebagai operator energi dalam persamaan Schrödinger.

3. Contoh Penerapan Mekanika Hamiltonian

  • Analisis osilator harmonik kuantum: Digunakan dalam mekanika kuantum untuk memahami spektrum energi sistem kuantum sederhana.
  • Simulasi sistem dinamis dalam ruang fase: Berguna dalam memahami perilaku sistem kompleks seperti sistem bintang biner dan dinamika partikel dalam medan elektromagnetik.
  • Studi kekacauan dalam fisika non-linier: Menganalisis sistem yang mengalami transisi dari keteraturan ke kekacauan, seperti cuaca dan turbulensi fluida.

—

Perbedaan Utama antara Mekanika Lagrangian dan Hamiltonian

1. Pendekatan Energi yang Berbeda

  • Mekanika Lagrangian berfokus pada perbedaan antara energi kinetik dan energi potensial suatu sistem.
  • Mekanika Hamiltonian berfokus pada energi total sistem yang dinyatakan dalam bentuk koordinat dan momentum.

Ilustrasi Sederhana

Jika kita mengamati seorang pelari:

  • Mekanika Lagrangian melihat bagaimana energi kinetik dan potensial berubah sepanjang lintasan pelari.
  • Mekanika Hamiltonian melihat bagaimana posisi dan momentum pelari berubah seiring waktu dalam ruang fase.

2. Variabel yang Digunakan

  • Mekanika Lagrangian menggunakan koordinat umum (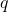q) dan kecepatannya (\dot{q}).
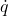  • Mekanika Hamiltonian menggunakan koordinat umum (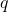q) dan momentumnya (p).

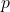Ilustrasi Sederhana

Mekanika Lagrangian seperti menggunakan peta jalur perjalanan, sedangkan mekanika Hamiltonian seperti menggunakan GPS yang melacak posisi dan kecepatan secara bersamaan.

3. Ruang Analisis yang Digunakan

  • Mekanika Lagrangian bekerja di ruang koordinat (konfigurasi sistem).
  • Mekanika Hamiltonian bekerja di ruang fase (posisi dan momentum sistem).

Ilustrasi Sederhana

Mekanika Lagrangian seperti melihat jalur sebuah mobil di peta, sedangkan mekanika Hamiltonian seperti melihat kecepatan dan posisi mobil dalam grafik dua dimensi.

—

Kesimpulan

Mekanika Lagrangian dan Hamiltonian adalah dua pendekatan fundamental dalam fisika klasik yang digunakan untuk mempelajari dinamika sistem mekanik:

  • Mekanika Lagrangian berfokus pada energi kinetik dan potensial, menggunakan persamaan Euler-Lagrange untuk menentukan lintasan sistem.
  • Mekanika Hamiltonian menggunakan energi total dalam koordinat dan momentum, dengan persamaan Hamilton untuk menganalisis dinamika sistem dalam ruang fase.

Mekanika Lagrangian lebih cocok untuk sistem dengan koordinat yang kompleks, sementara mekanika Hamiltonian lebih berguna dalam fisika kuantum dan analisis sistem dinamis. Dengan memahami perbedaan ini, kita dapat memilih pendekatan yang paling sesuai untuk berbagai masalah dalam fisika teoretis dan terapan.